Enunciado
Física - Young and Freedman - Vol 1- Ed: 14º - Capítulo 3.Problemas - Ex. 57
Um gafanhoto salta para o ar da beirada de um rochedo vertical, como mostra a Figura . Determine (a) a velocidade inicial do gafanhoto e (b) a altura do rochedo.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar (a) a velocidade inicial do gafanhoto e (b) a altura do rochedo do qual o gafanhoto salta, segundo a figura abaixo:
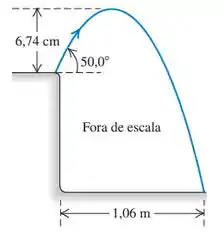
A partir da figura, podemos ler a altura máxima e distância máxima horizontal alcançada pelo gafanhoto. Sabendo que sua aceleração é para baixo, podemos encontrar sua velocidade inicial e a altura do rochedo (as variáveis alvo).
Vamos considerar as coordenadas com a origem no solo e para cima, . Assim, vamos usar a equação de Torricelli para determinar a velocidade inicial :
E as equações cinemáticas abaixo, para determinar o tempo de queda e a altura do rochedo :
Vamos lá!
Passo 2
a) A componente vertical da velocidade é zero no ponto mais alto da trajetória. Então, temos . Assim, usando a equação de Torricelli:
Isolando a velocidade inicial :
E substituindo os dados do enunciado, temos:
Mas essa é a componente vertical da velocidade inicial , que é dada por:
Onde é o ângulo de lançamento. Assim, isolando na equação e substituindo os valores dados, vamos ter:
Passo 3
b) Agora vamos determinar a altura do rochedo, mas antes precisamos encontrar o tempo de queda do gafanhoto, que é igual ao tempo de subida. Pra isso, vamos usar a equação horária da posição no eixo horizontal :
Nossa distância horizontal é , a aceleração horizontal é nula () e a componente horizontal da velocidade inicial é dada por:
Então, isolando na equação da posição e substituindo os valores calculados, temos:
Passo 4
Agora sim, vamos descobrir a altura do rochedo. No eixo vertical, temos:
Onde é a altura que queremos encontrar, é a velocidade inicial na direção vertical e é o tempo calculado no passo anterior. Assim, substituindo os valores na equação, vamos ter:
Valeu, galera! Até a próxima! 😉