Uma caixa vazia desliza para baixo de uma rampa, começando com uma velocidade inicial e atingindo a base com uma velocidade v e uma energia cinética K. Alguns livros são colocados no interior da caixa de modo que sua massa fica multiplicada por quatro. A resistência do ar é desprezível e o coeficiente de atrito cinético é constante. Novamente começando com uma velocidade inicial no topo da rampa, qual seria sua velocidade e sua energia cinética base da rampa? Explique o raciocínio usado na solução.

E como o trabalho realizado pela força gravitacional é dado pela eq (7.3):

E como a energia cinética é dada por:

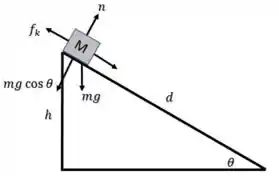
Primeiro, aplicamos a segunda lei de Newton e a segunda lei de Newton ao engradado na direção vertical, então temos:

Portanto, a força de atrito cinético atuando sobre o caixote é:

Suponha que a distância percorrida pelo caixote ao longo da rampa seja d, e considerando que a direção do deslocamento seja a direção positiva, de modo que o trabalho realizado pela força de atrito seja:

A partir do triângulo retângulo, descobrimos que a altura da rampa é dada por:

Tomando o nível zero zero da energia potencial para estar na parte inferior da rampa, temos:

Substituindo os valores que temos na equação (1), obtemos:

Como podemos ver, a velocidade final não depende da massa do caixote; portanto, não importa se sua massa é quádrupla ou não.

A razão por trás disso é que todos os termos da equação (1) dependem da massa e, portanto, se cancelam.

A velocidade final não depende da massa do engradado; portanto, não importa se sua massa quadruplicou ou não.

A razão por trás disso é que todos os termos da equação (7.8) dependem da massa e, portanto, se anulam.