Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 4

Calcule o ângulo entre duas diagonais internas (que passam por dentro) de um cubo, utilizando o produto escalar entre vetores.

Passo 1

É importante começar esboçando a situação pra direcionar melhor sua estratégia de resolução, então saca só como fica

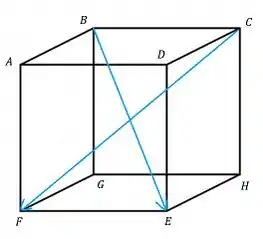
Transformamos essas 2 diagonais em vetores e queremos calcular o ângulo entre eles, lets bora?

Passo 2

  • Queremos a n g   (   B E ⃑   ,   C F ⃑ )

  • Vamos escrever B E ⃑   como B G ⃑ + G E ⃑ e C F   ⃑   como C H ⃑ + H F ⃑

  • G E ⃑ = B D ⃑ = B C ⃑ + C D ⃑

→

B E ⃑ = B G ⃑ + C D ⃑ +   B C ⃑

= B G ⃑ + G F ⃑ +   B C ⃑  

= B F ⃑ + B C ⃑

  • C H ⃑ = B G ⃑  

  • H F ⃑ = C A ⃑ = C B ⃑ + B A ⃑ =   - B C ⃑ + C D ⃑

    • →

    C F ⃑ = B G ⃑ + C D ⃑ -   B C ⃑

    =   B G ⃑ + G F ⃑ -   B C ⃑  

    = B F ⃑ - B C ⃑

    Como, por definição, a ⋅ b = a b c o s θ   →

    c o s θ = a ⋅ b a b

    Aplicando a nossos vetores   B E ⃑   e   C F ⃑

    c o s θ =     B E ⃑ ⋅ C F ⃑ B E ⃑ C F ⃑

    Aplicando as equivalências que fizemos no começo temos

    c o s θ = ( B F ⃑ + B C ⃑ ) ⋅ ( B F ⃑ - B C ⃑ ) B F ⃑ + B C ⃑ B F ⃑ - B C ⃑

    = B F ⃑ ⋅ B F ⃑ -   B C ⃑ ⋅ B C ⃑ B F ⃑ + B C ⃑ B F ⃑ - B C ⃑

    Como o ângulo entre um vetor e ele mesmo é 0, então seu produto escalar fica

    a ⋅ a = a a c o s 0 °

    = a 2  

    Aplicando na nossa equação anterior, vai ficar assim

    c o s θ = B F ⃑ 2 -   B C ⃑ 2 B F ⃑ + B C ⃑ B F ⃑ - B C ⃑

    Passo 3

    Para descobrir nosso ângulo falta só calcular esses valores, mas como?

  • Vamos começar percebendo que B C ⃑ é um lado do cubo, então ‖ B C ⃑ ‖ = l

  • B F ⃑ é a diagonal de uma face, por Pitágoras temos ‖ B F ⃑ ‖ = l 2

  • Já os outros 2 vetores são nossas diagonais em azul na figura, podemos calcular seu módulo por Pitágoras igualmente sendo seu tamanho igual a l 2 + l 2 + l 2 = l 3

Pronto, agora só é substituir os valores

c o s θ = l 2 2 -   l 2 l 3 2    

= l 2 3 l 2

= 1 3

→

θ = a r c o s 1 3 = 70,5 °

Resposta

θ = 70,5 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Verdadeiro ou falso: (a) O produto escalar não pode ter unidades. (b) Se o produto escalar de dois vetores não-nulos é zero, então eles são paralelos. (c) Se o produto escalar de dois vetores não-nulo
Verdadeiro ou falso: (a) O produto escalar não pode ter unidades. (b) Se o produto escalar de dois vetores não-nulos é zero, então eles são paralelos. (c) Se o produto escalar de dois vetores não-nulo
Verdadeiro ou falso: (a) O produto escalar não pode ter unidades. (b) Se o produto escalar de dois vetores não-nulos é zero, então eles são paralelos. (c) Se o produto escalar de dois vetores não-nulo
Verdadeiro ou falso: (a) O produto escalar não pode ter unidades. (b) Se o produto escalar de dois vetores não-nulos é zero, então eles são paralelos. (c) Se o produto escalar de dois vetores não-nulo
Dez polegadas de neve caíram durante a noite e você deve retirá-la da entrada de sua garagem, que tem o comprimento de 50 ft (figura abaixo). Estime quanto trabalho você deve realizar sobre a neve par