Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 6.1 - Ex. 21
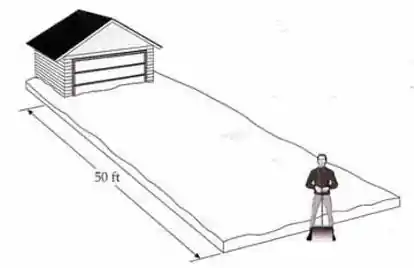
Dez polegadas de neve caíram durante a noite e você deve retirá-la da entrada de sua garagem, que tem o comprimento de 50 ft (figura abaixo). Estime quanto trabalho você deve realizar sobre a neve para completar a tarefa. Faça hipóteses plausíveis para os valores que forem necessários (a largura da entrada, por exemplo) e justifique cada hipótese.
Passo 1
O trabalho que você vai realizar é igual à variação de energia potencial gravitacional da neve:
Só que massa é densidade vezes volume ():
Passo 2
Agora vamos aos chutes: vamos assumir que a largura da garagem é 18 pés (18 ft) e que a densidade da neve seja . Agora vamos chutar o volume da neve:
O valor 10/12 é meio estranho, mas facilita a conta. Temos:
Passo 3
Agora joga tudo na equação:
Resposta
Exercícios de Livros Relacionados
Dados dois vetores não-nulos, A → e B → , mostre que se A → + B → = A → - B → , então A → ⊥ B → . (b) Dado o vetor A → = 4 i ^ - 3 j ^ , encontre um vetor no plano xy que seja perpendicular a A → e qu
No Capítulo 8, introduziremos um novo vetor associado a uma partícula, a sua quantidade de movimento linear, simbolizado por p → . Matematicamente, ele está relacionado à massa m e à velocidade v → da
Os vetores unitários A ^ e B ^ estão no plano xy. Eles formam os ângulos θ 1 e θ 2 , respectivamente, com o eixo +x. (a) Use trigonometria para encontrar diretamente as componentes x e y dos dois veto
(a) Seja A → um vetor constante, no plano xy, com sua origem na origem do sistema de coordenadas. Seja r → = x i ^ + y j ^ um vetor do plano xy que satisfaz à relação A → ∙ r → = 1 . Mostre que os pon
Uma partícula se move em um círculo centrado na origem, a magnitude de seu vetor posição r → sendo constante. (a) Derive r → ∙ r → = r 2 = c o n s t a n t e em relação ao tempo, para mostrar que v → ∙