Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 7.Problemas - Ex. 20

Num parque de diversões, um carrinho desce de uma altura h para dar a volta no loop de raio R indicado na figura. a) Desprezando o atrito do carrinho com o trilho, qual menor valor h 1 de altura necessário para permitir o carrinho dar a volta toda? b) Se R < h < h 1 , o carrinho cai do trilho num ponto B, quando ainda falta percorrer mais um ângulo θ   para chegar até o topo A (Fig). Calule θ . c) Que acontece com o carrinho para h < R ?

Passo 1

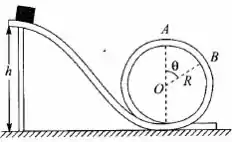
  1. Fala galera! No ponto A o carrinho vai estar submetido a 2 forças. A normal que o trilho faz sobre ele e o peso, beleza? Vê aqui como fica

    2. Essas são as forças responsáveis pelo giro e compõem a resultante centrípeta, belê?

    F c p = P + N

    Se a intenção é achar a altura mínima para fazer o loop, buscamos também a velocidade mínima que o carrinho precisa pra dar essa volta sem cair. Na situação limite nossa normal vai ser 0, que é quando o carrinho estiver perdendo o contato com os trilhos no ponto A. Então fica assim

    F c p = P

    →

    m v 2 R = m g

    →

    v 2 = R g

    Pronto, desde o início da descida até o ponto A nossa energia cinética variou isso aqui ó

    Δ K =   m v 2 2 - 0

    = m R g 2

    Sabemos que isso equivale ao trabalho exercido pela força gravitacional   W g

    W g = Δ K =   - Δ U g

    = U i - U f

    = m g h 1 - m g 2 R

    Substituindo o valor da variação de energia cinética,

    m g h 1 - m g 2 R = m g R 2

    →

    m g h 1 = 5 2 m g R

    →

    h 1 = 5 2 R

    Passo 2

  2. Uma observação importante é que para o bloco perder contato sua velocidade no ponto B não é 0, mas sim aquela que zera a normal da superfície, belê?

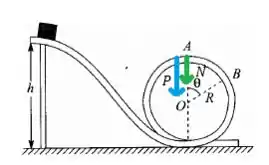
    3. Usando o mesmo raciocínio da Letra a) temos

    F c p = P r a d i a l

    Mas como vamos calcular a componente radial do peso? Chega junto aqui.

    Esse ângulos θ   são alternos internos e por isso são iguais, assim fica tranquilo perceber que aquela projeção radial é P c o s θ .

    F c p = P c o s θ

                          →

    v 2 R = g c o s θ

                            →

    v = g R c o s θ

    Vamos calcular a energia mecânica nesse ponto B e simplesmente igualar à energia mecânica inicial já que o sistema é conservativo. E aí a gente mata a alternativa, vem comigo!

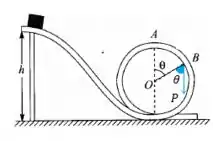
    Só falta calcular a altura do ponto B, saca só o esquema

    h ' = R + R c o s θ

    = R ( 1 + c o s θ )

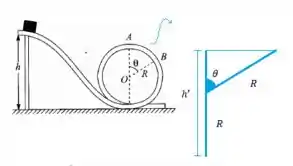
    Então nossa energia mecânica fica assim

    E b = 1 2 m v b 2 +   m g h '

    = 1 2 m g R c o s θ + m g R ( 1 + c o s θ )

    = 3 2 m g R c o s θ + m g R

    Já no ponto de lançamento termos

    E = m g h

    Pela conservação de energia,

    m g h =   3 2 m g R c o s θ + m g R

    →

    h = R 3 2 c o s θ + 1

    →

    h R - 1 = 3 2 c o s θ

    →

    c o s θ = 2 3 h R - 1  

    →

    θ = a r c o s 2 3 h R - 1  

    Passo 3

  3. Nesse caso o bloco não tem energia potencial pra ultrapassar metade do arco e adquirir velocidade horizontal para a esquerda, então o bloco simplesmente fica subindo e descendo entre o ponto máximo da trajetória e o ponto de lançamento ao invés de sair voando pro meio e depois dar de cara com o chão como no caso anterior.

Resposta

a )   h 1 = 5 R 2

b ) θ = a r c o s 2 3 h R - 1  

c )   c a r r i n h o   f i c a   o s c i l a n d o  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um pacote de 2,0 kg inicialmente em repouso é abandonado sobre um plano inclinado de 53,1°, a uma distância de 4,0 m de uma mola com constante de 120 N/m presa à base do um plano (Figura 7.43). Os coe
Uma partícula com massa m sofre ação de uma força conservativa e se desloca ao longo de uma trajetória dada por x = x 0 cos ⁡ ω 0 t e y = y 0 sin ⁡ ω 0 t , onde x 0 , y 0 e ω 0 são constantes. (a) Ach
Um sistema consiste em três partículas, cada uma de massa 5,00 g, localizadas nos vértices de um triângulo equilátero com lados de 30,0 cm.a.Calcule a energia potencial que descreve as interações grav
A energia potencial de um sistema de duas partículas separadas por uma distância r é determinada por U ( r )=A / r , em que A é uma constante. Encontre a força radial F r → que cada partícula exerce s
Uma função energia potencial para um sistema no qual uma força bidimensional age é U=3 x 3 y–7 x . Encontre a força que age nesse ponto ( x ,y ) .