Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 9.Problemas - Ex. 7
Calcule a indutância mútua entre uma espira circular de raio e um fio retilíneo coplanar muito longo que transporta uma corrente e está à distância b do centro da espira.
Passo 1
Se liga! Lembra que a indutância é
Vamos começar fazendo o fluxo que o fio causa na espira.
Primeiro precisamos lembrar que o campo do fluxo magnético é dado por
e que o campo relacionado ao fio é
Olha a figura!
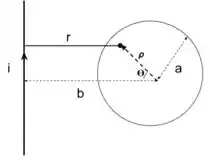
Podemos reparar que a distância , pode ser escrito como
A área dependerá de e do ângulo ,
onde e .
Passo 2
Agora só precisamos calcular o fluxo resolvendo a integral a seguir.
Resolvendo essa integral, vamos obter
Passo 3
Substituindo as informações na expressão da indutância, temos
Resposta
Exercícios de Livros Relacionados
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
( a ) Calcule o fluxo magnético através do anel retangular mostrado na figura 28-43. b Determine sua resposta para a = 5,0c m ,b = 10 c m ,d = 2,0 c meI = 20 A .
Um cabo coaxial consiste em dois condutores cilíndricos de paredes muito finas com raios r 1 e r 2 (Figura 28-63). As correntes nos cilindros interno e externo são iguais em magnitude mas têm sentidos
Uma bobina retangular uniforme com massa total igual a 212 g e dimensões de 0,500 m 1,00 m está orientada no sentido perpendicular a um campo magnético uniforme de 3,00 T (Figura E27.43). Uma corrente
Uma espira plástica circular de raio R e carga positiva q está uniformemente distribuída em torno da circunferência da espira. A seguir, a espira é girada em torno de seu eixo central, perpendicular a