Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 10.Problemas - Ex. 11a
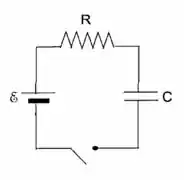
No circuito da figura, a chave é ligada em , como capacitor descarregado.
- Ache a corrente em função do tempo.
Passo 1
Vamos lá!
Pela configuração podemos ver escrever que
Derivando em relação a temos
Lembrando que
Passo 2
Aplicando este resultado na equação anterior, temos
Integrando dos dois lados, onde e , temos
Aplicando a exponencial dos dois lados, temos
Onde . Portanto
Resposta
Exercícios de Livros Relacionados
Um resistor de 3,00 M Ω e um capacitor de 1,00 μF são ligados em série com uma fonte ideal de força eletromotriz ε = 4,00 V . Depois de transcorrido 1,00 s, determine (a) a taxa de aumento da carga do
Um capacitor de 1,0 μF com uma energia inicial armazenada de 0,50 J é descarregado através de um resistor de 1,0 M Ω . (a) Qual é a carga inicial do capacitor? (b) Qual é a corrente no resistor quando
No circuito da Fig. 27-65, ε = 1,2 k V , C = 6,5 μ F e R 1 = R 2 = R 3 = 0,73 M % O M E G A . Com o capacitor C totalmente descarregado, a chave S é fechada bruscamente no instante t = 0 . Determine,
Um capacitor C inicialmente descarregado é carregado totalmente por uma fonte de força eletromotriz constante ε ligada em série com um resistor R. (a) Mostre que a energia final armazenada no capacito
Na Fig. 27-73, R 1 = 5,00 Ω , R 2 = 10,0 Ω , R 3 = 15,0 Ω , C 1 = 5,00 μ F , C 2 = 10,0 μ F e a fonte ideal tem uma força eletromotriz ε = 20,0 V . Supondo que o circuito se encontra no regime estacio