Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 28.1 - Ex. 81

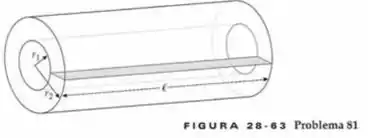
Um cabo coaxial consiste em dois condutores cilíndricos de paredes muito finas com raios r 1 e r 2 (Figura 28-63). As correntes nos cilindros interno e externo são iguais em magnitude mas têm sentidos opostos. Calcule o fluxo através da área retangular de lados l e r 2 - r 1 entre os condutores mostrados na figura 28-63. Use a relação entre o fluxo e a correntes ϕ m = L I para mostrar que a auto-indutância por unidade de comprimento do cabo é dada por   L l = μ 0 2 π ⋅ ln ⁡ r 2 r 1 .

Passo 1

E aí bonit@s, como vocês estão?

Se liga só na estratégia que vamos utilizar para resolver essa questão: podemos usar a definição para expressar o fluxo magnético através de um elemento retangular de área d A e então integrar de r = r 1   a   r = r 2 para expressar o fluxo total através da região, depois substituir em L = ϕ m / I .

Passo 2

Considere uma faixa de comprimento unitário l largura d r a uma distância r do eixo. O fluxo através desta área é dado por:

d ϕ m = B d A = B l d r

Aplicando a lei de Ampère para expressar o campo magnético a uma distância r do eixo teremos

2 π r B = μ 0 I → B = μ 0 I 2 π r

Substituindo B na expressão anterior vamos ter

d ϕ m = μ 0 I 2 π r ⋅ l d r

Passo 3

Agora para finalizar o problema vamos integrar de r 1   a   r 2 obtendo

ϕ m = μ 0 I l 4 π ⋅ ∫ r 1 r 2 d r r = μ 0 I l 4 π ⋅ ln ⁡ r 2 r 1  

Agora usando a definição de auto indutância temos que

L = ϕ m I = μ 0 I l 4 π ⋅ ln ⁡ r 2 r 1 I = μ 0 l 4 π ⋅ ln ⁡ r 2 r 1

Passando l dividindo ficaremos com

L l = μ 0 4 π ⋅ ln ⁡ r 2 r 1

Pronto, está resolvido nosso problema.

Resposta

D e m o n s t r a ç ã o

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um condutor cilíndrico longo com raio R e comprimento L conduz uma corrente I . Determine o fluxo magnético por unidade de comprimento através da área indicada na Figura 28-44.
Um longo solenoide tem n voltas por unidade de comprimento, raio R 1 e conduz uma corrente I . Uma bobina circular de raio R 2 e com N voltas é coaxial ao solenoide e está equidistante de suas extremi
Uma bobina circular tem 15,0 voltas, raio de 4,0c m e está em um campo magnético uniforme de 4,0k G na direção + x . Determine o fluxo através da bobina quando a normal unitária do plano da bobina é a
Determine o fluxo magnético através de um solenoide de 400 voltas que tem comprimento igual a 25,0c m , raio igual a 1,00c m e conduz uma corrente de 3,00 A .
( a ) Calcule o fluxo magnético através do anel retangular mostrado na figura 28-43. b Determine sua resposta para a = 5,0c m ,b = 10 c m ,d = 2,0 c meI = 20 A .