Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 8.Problemas - Ex. 5
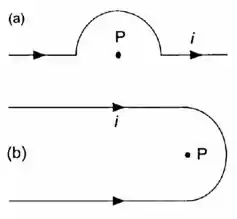
Nas figs. (a) e (c), as porções retilíneas dos fios são supostas muito longas e a porção semicircular tem raio . A corrente tem intensidade . Calcule o campo , em módulo, direção e sentido, no centro da porção semicircular, em ambos os casos.
Passo 1
Se liga! Vamos primeiro visualizar o problema!
Podemos perceber que as correntes causadas pela parte reta estão indo na direção do ponto. Sendo assim, usando o argumento que
podemos dizer que o campo produzido pela parte reta na figura (a) é zero.
Passo 2
Agora vamos analisar a semicircunferência na figura (a). Sabemos que
Como temos uma semicircunferência adotaremos que
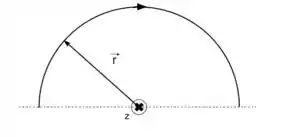
Como podemos ver . Agora precisamos integrar o campo para achar a contribuição de todo o segmento. Sendo assim
Pela regra da mão direita podemos ver que o campo está entrando na direção .
Sendo assim, podemos escrever
Passo 3
Para a figura (b), a parte da semiesfera nos dá o mesmo valor da semiesfera da figura (a).
Passo 4
Para os fios da figura (b), temos que pesar que o campo produzido por cada segmento provoca um campo cuja intensidade é a metade do campo provocado por um fio infinito. Ou seja
Como são dois fios
Agora só precisamos somar o campo dos fios retilíneos com o provocado pelo segmento da semicircunferência.
Pela regra da mão direita, todos os vetores estão apontando para dentro de . Portanto