Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 12.Problemas - Ex. 5

Calcule o momento de inércia de um cone circular reto homogêneo, de massa M e raio da base R , em relação ao eixo do cone. Sugestão considere o cone como uma pilha de discos cirulares de alturas infinitésimas e raios decrescentes.

Passo 1

Primeiro vamos fazer uma ilustração pra facilitar a nossa vida, se liga só:

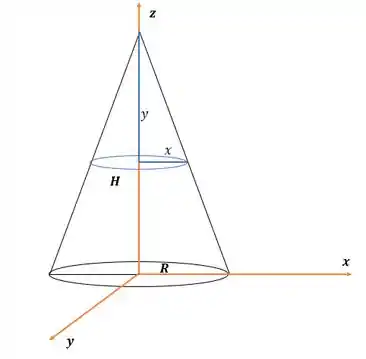
Pela dica do enunciado vamos pegar discos circulares de altura infinitesimal. Para um disco, temos:

I d i s c o = M r 2 2

Logo,

I = ∫ x 2 d m 2

Usando a densidade volumétrica:

d m = ρ d V

Além disso,

d V = π x 2 d y   ;   ρ = M 1 3 π R 2 H

Portanto,

d m = M 1 3 π R 2 H ⋅ π x 2 d y = 3 M R 2 H x 2 d y

Passo 2

Da semelhança de triângulo, tem-se:

x R = y H → x = y R H

Logo,

d m = 3 M R 2 H ⋅ y R H 2 d y

Arrumando as coisas

d m = 3 M H 3 y 2 d y

Passo 3

Para o momento de inércia:

I = 1 2 ⋅ ∫ x 2 d m

Então, I = 1 2 ⋅ ∫ 0 H y R H 2 3 M H 3 y 2 d y

Fazendo as simplificações:

I = 3 M R 2 2 H 5 ⋅ ∫ 0 H y 4 d y → I = 3 M R 2 2 H 5 ⋅ H 5 5

Portanto,

I = 3 M R 2 10

Resposta

I = 3 M R 2 10

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Equação (9.20) para calcular o momento de inércia de uma barra delgada de massa M e comprimento L em relação a um eixo perpendicular à barra e passando pela sua extremidade.
Uma barra delgada de comprimento L possui massa por unidade de comprimento variando a partir da extremidade esquerda, onde x = O, de acordo com dm/dx = gama x, onde gama é constante com unidades de kg
Use a Equação (9.20) para calcular o momento de inércia de um disco maciço, uniforme, de raio R e massa M em relação a um eixo perpendicular ao plano do disco passando pelo seu centro.
Centro de massa de um objeto com massa distribuída. Qual é o trabalho realizado por um lutador para elevar o centro de massa de seu oponente de 120kg até uma distância vertical igual a 0.700m?
Suponha que o cilindro maciço do dispositivo descrito no Exemplo 9.9 (seção 9.5) seja substituído por uma casca cilíndrica com o mesmo raio R e com a mesma massa M. O cilindro é ligado ao eixo por mei