Caminhando à beira de um lago, você encontra uma corda presa a um galho forte de uma árvore que está acima do nível do chão. Você decide usar a corda para se balançar sobre o lago. A corda está um pouco frágil, mas aguenta o seu peso. Você estima que a corda pode se romper se a tensão é maior do que o seu peso. Você segura a corda em um ponto a partir do galho e se move para trás para se balançar sobre o lago. (Adote, para você próprio, o modelo de uma partícula pontual presa à corda a do galho.) Qual é o ângulo máximo inicial seguro entre a corda e a vertical para o qual a corda não se romperá durante o movimento? (b) Se você começa nesse ângulo máximo, e a superfície do lago está abaixo do nível do chão, com qual rapidez você vai entrar na água se você soltar a corda quando ela está na vertical?
Passo 1
(a) Vamos definir o zero da nossa energia potencial como estando na altura da superfície do lago:
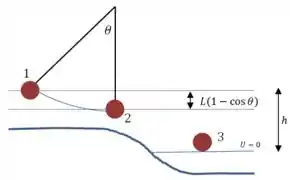
Vamos aplicar a conservação de energia entre os pontos e :
E vamos resolver essa equação para encontrar :
Passo 2
Agora precisamos encontrar a rapidez máxima que garante que a corda não se romperá durante o movimento.
Nesse caso máximo, a tensão sobre a corda estará exatamente no limite sugerido:
Como podemos relacionar isso com a rapidez ? Bom, entre e , a pessoa descreve uma trajetória circular, então deve haver uma resultante centrípeta:
E então:
E substituindo isso na expressão que escrevemos para o ângulo:
E usando uma massa de para a pessoa:
Passo 3
(b) Agora vamos aplicar conservação de energia entre os pontos e para encontrar a rapidez :
Mas nós sabemos que , então:
E qual é altura que separa os pontos e (superfície do lago)?
O enunciado diz que a superfície do lago está abaixo do chão.
E no ponto inicial, você está segurando a corda a de distância de um galho que está acima do chão, formando um ângulo de com a vertical.
Portanto a distância vertical entre você e o galho é:
Então a altura que separa você do nível do chão é:
E como o lago está abaixo do nível do chão, a sua distância vertical até o lago é:
Substituindo isso na expressão de cima:
Resposta
(a) .
(b) .