Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 7.1 - Ex. 88
Um reboque para esquiadores está sendo desenhado, para uma nova área de prática de esqui. Ele deve ser capaz de puxar um máximo de esquiadores em uma subida de , inclinada de acima da horizontal, com uma rapidez de . O coeficiente de atrito cinético entre os esquis e a neve vale, tipicamente, . Como gerente de instalações, você encomendaria ao fabricante um motor com qual potência, se a massa média de um esquiador é Suponha que você deve estar preparado para qualquer emergência, encomendando uma potência maior do que o mínimo calculado.
Passo 1
Vamos começar representando a situação por um diagrama:
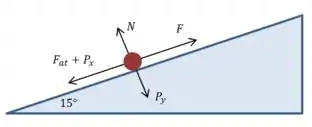
Como os esquiadores sobem o plano com rapidez constante, nós podemos garantir que as forças estão em equilíbrio em todas as direções. Então:
E usando outra equação de equilíbrio, podemos afirmar que , então:
Passo 2
Beleza, já temos uma expressão para a força, agora vamos calcular o trabalho realizado por ela, e relacionar isso com a potência do reboque:
Onde é a distância total a ser percorrida () e é a rapidez (). Agora, voltando à expressão que encontramos no passo anterior, o trabalho da força é:
Então:
Agora vamos igualar isso à expressão que escrevemos logo antes:
Passo 3
Mas essa é apenas a potência mínima necessária, o enunciado pediu para adicionarmos uma “margem de segurança” de de potência acima do mínimo.
Então:
Agora vamos substituir os valores numéricos, lembrando que temos que considerar a massa de esquiadores de cada:
Resposta
Encomendaria um motor com potência de .