Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 9ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 9º - Capítulo 24.5 - Ex. 7
O campo elétrico em uma certa região do espaço tem componentes e . O ponto A está no eixo y, em y = 3,00 m, e o ponto B está no eixo x, em x = 4,00 m. Qual é a diferença de potencial ?
Passo 1
Galera, pra calcular a diferença de potencial, a famosa ddp, a gente usa essa fórmula aqui:
Onde:
- é a diferença de potencial;
- é o campo elétrico e
- é a derivada desse comprimento do caminho.
Aquele caminho ali na integral pode ser qualquer caminho ligando os pontos A e B. Pode ser qualquer caminho? Pode, porque a força elétrica é o que a gente chama de conservativa, ou seja, independe da trajetória. Qualquer caminho é fácil de calcular? Não. Então nossa missão é achar um caminho que facilite nossa integral, que seja fácil de calcular.
Passo 2
A gente vai pegar esse caminho aqui oh:
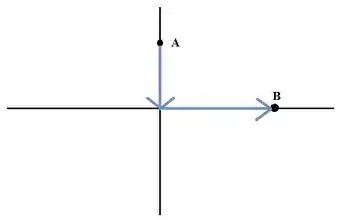
Aí a gente divide a integral em duas etapas: de A até a origem e da origem até B:
- De A até a origem:
- Da origem até B:
Só que no eixo y.
Isso faz com que a diferença de potencial seja igual a 0.
No eixo x, o campo é . Vamos integrar no eixo , logo:
Aí fica assim:
Como vamos da origem até o ponto , os limites de integração são do 0 até :
Passo 3
Agora some as contribuições: