Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 29.Problemas - Ex. 67
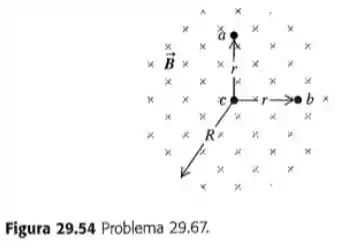
O campo magnético em todos os pontos de uma região circular de raio é uniforme e está direcionado para o interior do plano da página, como indicado na figura 29.54. (Essa região poderia ser a seção reta de um solenoide reto longo.) Sabendo que o campo magnético está crescendo com uma taxa , determine o módulo, a direção e o sentido das forças magnéticas que atuam sobre uma carga nos pontos , indicado na figura. ( O ponto está a uma distância acima do centro da região, o ponto está a uma distância do lado direito do centro da região e o ponto está no centro da região).
Passo 1
Para resolvermos o problema vamos utilizar o fato de que
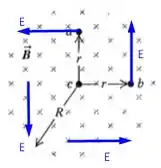
Para o círculo concêntrico de raio e então aplicaremos , tomando entrando na folha, semelhante a . Bom, primeiramente, podemos ver que aumentando nós temos , isso implica que nossa integral terá como resultado um valor negativo. Isso significa que é tangente ao círculo no sentido anti-horário como podemos ver na imagem abaixo
Aplicando vamos ter
Igualando ambas as equações acima teremos
Agora, temos tudo o que é necessário para encontrarmos o que a questão nos pede para cada um dos pontos.
Passo 2
Sendo assim, começando pelo ponto vamos ter
Onde está para a esquerda na mesma direção de desde que seja positiva. Da mesma forma vamos proceder para o ponto mas no caso dele vamos ter apontado para cima seguindo o campo elétrico em e seu valor em módulo será igual ao ponto . Por fim, para o ponto nós temos que o que vai implicar um campo elétrico nulo e consequentemente .
Resposta