Em um canteiro de obras, um balde de concreto de está suspenso por um cabo leve (porém forte), que passa sobre um polia leve sem atrito e está conectado a uma caixa de sobre um teto horizontal (Figura 7.29). O cabo puxa horizontalmente a caixa, e um saco de cascalho de repousa sobre o topo da caixa. Os coeficientes de atrito entre a caixa e o teto são indicados. (a) Ache a força de atrito sobre o saco de cascalho e sobre a caixa. (b) Subitamente, um operário apanha o saco de cascalho. Use a conservação de energia para determinar a velocidade do balde após ele ter descido partindo do repouso. (Você pode conferir sua resposta solucionando este problema usando as leis de Newton.)
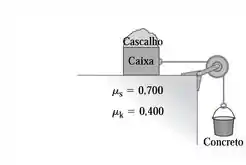
Passo 1
Primeira coisa é definir o sistema de coordenada e as forças que atuam no problema.
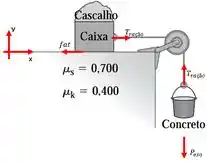
Feito a analise das forças, agora aplicaremos a segunda lei sobre a caixa e sobre o saco de cascalho.
Passo 2
Como inicialmente o sistema se escontra em repouso, podemos considerar o conjunto Caixa + Cascalho um corpo único. Desta forma, teremos que a somatória das forças no corpo será
Implicando que
Desta forma apenas temos que descobrir quem é .
Analisando o Concreto pendurado pela corda, temos que, por estar em repouso, a somatória de forças sobre ele também será nula, ou seja,
Assim a força de atrito sobre a Caixa + Cascalho será de
Mas qual seria a força necessária para mover a Caixa + Cascalho ? Podemos responder essa pergunta analisando apenas a força de atrito. Por estar em repouso, o coeficiente de atrito a ser considerado será o estático .
Logo a força necessária para remover a Caixa + Cascalho do repouso é muito maior da força que está sendo aplicada pela Tração.
Passo 3
Ao remover o saco de Cascalho da caixa, temos que a força necessária para segurar a Caixa cai para , desta forma ela deixa seu estado de repouso.
Entretanto podemos resolver essa questão por conservação de energia. Assim vamos analisar a energia inicial e final ao movimento.
A Caixa se encontra em repouso inicialmente e nosso sistema de coordenado foi definido ao piso da Caixa, desta forma tanto sua energia cinética quando potencial serão nulas inicialmente. Para o balde de concreto temos que ele se encontra a uma distância entretanto também se encontra em repouso, logo a energia inicial do sistema será
Agora vamos analisar as energias finais do sistema. A caixa começa a se mover para a direita e o balde para baixo. A energia potencial da caixa será sempre nula neste problema, visto que ela não deixa a plataforma que se encontra. Porém temos que o balde desceu um pouco mais do que se encontrava inicialmente, assim temos que
Como a corda é o que limita o movimento, temos que a velocidade tanto da caixa quando o balde serão as mesmas, ou seja
Podemos reescrever as energias da seguinte forma
Isolando temos
Prontinho!