Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 42
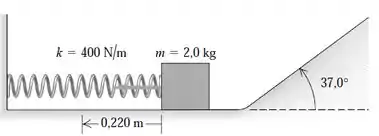
Um bloco de 2,0 kg é empurrado contra uma mola de massa desprezível e constante k=400 N/m, comprimindo a mola até uma distância igual a 0,220 m. Quando o bloco é libertado, ele se move ao longo de uma superfície horizontal sem atrito e sobe um plano inclinado de 37,0° (Figura 7.30).
a) Qual a velocidade do bloco enquanto ele desliza ao longo da superfície horizontal depois de abandonar a mola?
b) Qual a distância máxima que ele atinge ao subir o plano inclinado até parar antes de voltar para a base do plano?
Passo 1
Vamos utilizar o princípio da conservação de energia para tentar responder este problema.
Inicialmente dizemos que o bloco tinha uma velocidade inicial e uma energia potencial elástica por conta da mola. Dessa forma, toda essa energia potencial elástica será transformada em cinética e potencial gravitacional ao longo do percurso. Vamos ver como isso fica na prática!
Vamos aplicar a equação:
Somente a força e a gravidade da mola funcionam, então:
Vamos tomar na superfície horizontal.
Passo 2
- Igualando a energia potencial armazenada na mola à energia cinética do bloco:
- Usando métodos de energia diretamente, a energia potencial inicial da mola é igual ao potencial gravitacional final:
ou
Passo 3
ou
A energia total do sistema é constante. Inicialmente, é toda a energia potencial elástica armazenada na mola, então é toda energia cinética e, finalmente, toda energia potencial gravitacional.