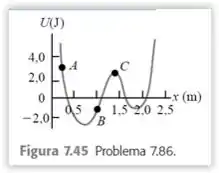
Uma única força conservativa paralela ao eixo atua sobre uma partícula que se desloca ao longo do eixo . A força corresponde ao gráfico de energia potencial indicado na . A partícula é libertada a partir do repouso no ponto A.

a) Qual a direção e o sentido da força que atua sobre a partícula no ponto A?

b) E no ponto B?

c) Para qual valor de x sua energia cinética é máxima?

d) Qual é a força que atua sobre a partícula no ponto C?

e) Qual o valor máximo de x atingido pela partícula durante seu movimento?

f) Para quais valores de x a partícula está em equilíbrio estável?

g) Onde ela está em equilíbrio instável?

Para o item (a), olhe cuidadosamente para o gráfico, é a energia potencial versus .

Inicialmente, a partícula estava em repouso, então a força só pode agir na direção da velocidade.

Isso significa que a energia potencial deve estar diminuindo.

Pelo gráfico, podemos ver que: No ponto A, a energia potencial diminui na direção positiva de .

Isso significa que a força inicial estava atuando na direção positiva de x.

Para o item (b), a inclinação é positiva, então a força é negativa. Pelo mesmo motivo do passo anterior (a força e a derivada de possuem sinais contrários):

Para o item (c), a energia cinética é máxima quando é um mínimo e isso acontece entre e . Então, vamos usar a aproximação que

Para o item (d), temos que a derivada no ponto C é zero, pois se trata de um ponto crítico (isso vem lá a disciplina de Cálculo para quem não lembra).

Isso porque a reta tangente à essa curva nesse ponto é horizontal. Com isso:

A força é nula nesse ponto!

Para o item (e), o é máximo quando . No ponto A, a energia cinética é zero (a partícula está em repouso), mas é negativo, logo:

Para que a energia potencial seja positiva, a energia cinética precisaria ser negativa, mas não existe energia cinética negativa; portanto, o objeto nunca pode estar em qualquer ponto em que a energia potencial seja maior que no ponto A.

Para o item (f), o equilíbrio é estável onde é um mínimo local, isso acontece depois do ponto C e antes de B, assim vamos dizer que temos equilíbrios estáveis em e .

Para o item (g), o equilíbrio é instável onde é um máximo local, o único potencial máximo e, portanto, o único ponto de equilíbrio instável, é o ponto C.