Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 7.Problemas - Ex. 40

Dois blocos com massas diferentes estão amarrados a cada extremidade de uma corda leve que passa sobre uma polia leve e sem atrito, que está suspensa a partir do teto. As massas são libertadas do repouso, e a mais pesada começa a descer. Após essa massa descer 1,20 m, sua velocidade é 3,0 m/s. Se a massa total dos dois blocos é 15,0 kg, qual é a massa de cada bloco?

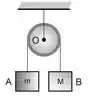
Passo 1

Primeiramente devemos analisar a energia inicial e final do sistema. Como partimos do repouso, temos que a energia inicial do sistema será nula. Posteriormente temos que uma das massa começa a descer e a outra subir. Como ambas as massas estão vinculadas por uma corda, a velocidade de amabas será igual, mas com sentidos diferentes.

Equacionando nosso problema temos que :

K 1 + U 1 + K 2 +   U 2 = 0  

m 1 + m 2 ⋅ v 2 2 + 1,20 m ⋅ g ⋅ m 1 - m 2 = 0

Passo 2

Sabemos que m 1 + m 2 = 15   k g , v = 3 m s e g = 9,80   m / s 2

Então temos que

15   k g 2 3,0 m s 2 + 1,20 m ⋅ 9,80 m s 2 ⋅ 2 m 1 - 15 k g = 0

Isolando m 1 , temos que

m 1 = 4,6   k g

Logo,

m 2 = 10,4   k g

Resposta

m 1 = 4,6   k g

e

m 2 = 10,4   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

30. A força resultante que atua sobre um corpo restringido ao eixo x , é dada por F x x = x 3 - 4 x . (A força está em newtons e x em metros.) Localize as posições de equilíbrio instável e estável. Mo
33. Uma barra reta de massa desprezível está montada sobre um pivô sem atrito, como mostrado na figura 7-38. Blocos de massa m 1 e m 2 estão presos à barra, nas distânica l 1 e l 2 .a) Escreva uma exp
35. Você projetou um relógio bem original, mostrado na Figura 7-40. Sua preocupação é que ele ainda não esteja pronto para o mercado, pela possibilidade de apresentar uma configuração de equilíbrio in
Uma bola de gude move-se ao longo do eixo Ox. A energia potencial é indicada na Figura 7.28. a) Para quais valores de x indicados no gráfico a força é igual a zero? b) Para quais valores de x indicado
A energia potencial entre dois átomos em uma molécula diatômica é dada por U r =a r 12 -b r 6 , onde r é a distância entre os átomos e a e b são constantes positivas. a) Determine a força F ( r ) que