Exercícios de Equilíbrios e Energia Potencial - Lista de Exercícios Resolvida
Questão 1
Uma partícula de massa pode se deslocar em uma dimensão, submetida a um potencial dado por em unidades do SI: em Joules (), e em metros ().
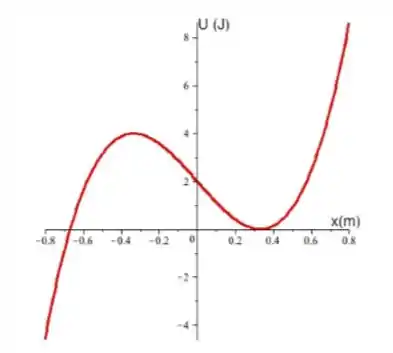
Determine a expressão da força atuando sobre a partícula em função da posição .
Calcule as posições de equilíbrio da partícula.
Determine as condições de equilíbrio em cada ponto, ou seja, se é estável, instável ou indiferente.
Se uma partícula de massa for deixada na condição de equilíbrio estável com velocidade de , ela realiza um movimento periódico? Justifique.
Ver solução completaQuestão 2
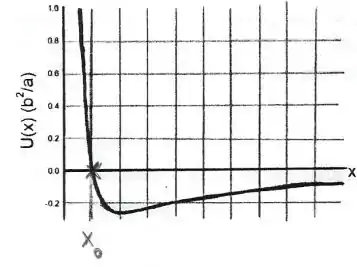
A energia potencial de ligação entre átomos de moléculas diatômicas pode ser descrita, dentro de certos limites, pelo gráfico ao lado, dado pela equação
onde é a distância entre os núcleos dos átomos, a e b são constantes. 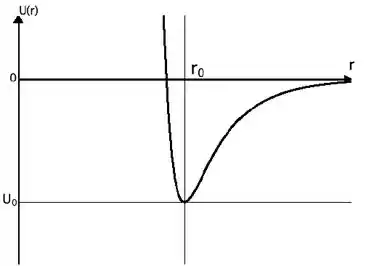
a) Qual a equação da força entre os átomos?
b) Determine a distância de equilíbrio .
c) Determine a energia potencial mínima .
Dê suas respostas somente em termos de e .
Ver solução completaQuestão 3
Uma partícula desloca-se ao longo do eixo , de unitario , sob ação de uma força conservativa , correspondente ao potencial , dado pelo gráfico da figura. Para este potencial, entre as alternativas abaixo, a única INCORRETA é
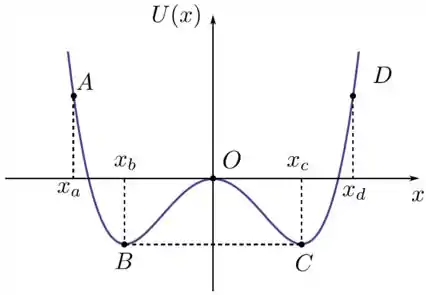
- Na posição a força sobre a particula é nula;
- Nas posições e tem-se a condição de equilíbrio estável;
- No deslocamento da particular de para o trabalho realizado pela força é negativo;
- No deslocamento da partícula de para a variação da energia cinética é ;
- Na posição o sentido da força é positivo.
Questão 4
Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa , correspondente a um potencial , dado pela figura abaixo. Para este potencial entre as opções abaixo a única incorreta é:
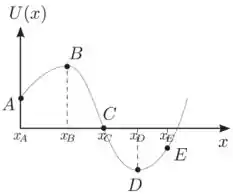
- Na posição a força sobre a partícula é nula;
- Na posição , tem-se a condição de equilíbrio estável;
- No deslocamento do corpo de para o trabalho realizado pela força é positivo;
- O sentido da força na posição é negativo;
- Na posição a força é nula.
Questão 5
Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa , correspondente a um potencial , dado pela figura abaixo. Para este potencial entre as opções abaixo a única incorreta é:
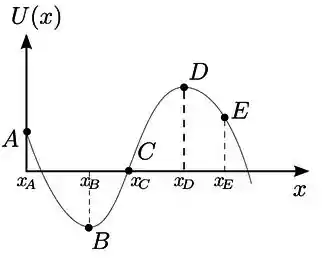
- Na posição a força sobre a partícula é nula;
- Na posição , tem-se a condição de equilíbrio instável;
- No deslocamento do corpo de para o trabalho realizado pela força é negativo;
- O sentido da força na posição é positivo;
- Na posição a força não é nula.
Questão 6
Um próton de massa se move em uma dimensão na presença de uma força cuja energia potencial é dada por:
Sendo e constantes positivas. O próton é liberado do repouso no ponto
a) Calcule .
b) Escreva qual(is) é(são) o(s) ponto(s) de equilíbrio, e classifique-o(s) como estável, instável ou indiferente, fundamentando a classificação.
c) Calcule a velocidade do próton em função da posição .
Ver solução completaQuestão 7
Um corpo de massa se move em uma dimensão ao longo do eixo . Sua energia potencial é dada por:
Onde é dado em metros e em joules. O gráfico representa a variação da energia potencial em função da distância. Caso seja necessário, use .
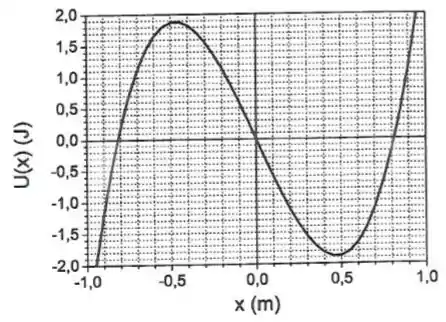
a) Calcule a força exercida sobre o corpo em função de .
b) Calcule a(s) posição(ões) de equilíbrio, marque-a(s) como ponto(s) de equilíbrio estável, instável ou indiferente. Justifique sua resposta.
c) Assumindo que o corpo esteja inicialmente no ponto de equilíbrio à direita da origem, a partir de qual valor para a velocidade o movimento deixa de ser oscilatório?
Ver solução completaQuestão 8
Uma partícula de massa pode se deslocar em uma dimensão, submetida a um potencial dado por em unidades do SI: em Joules (), e em metros ().
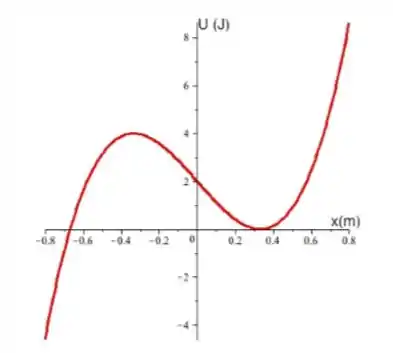
Determine a expressão da força atuando sobre a partícula em função da posição .
Calcule as posições de equilíbrio da partícula.
Determine as condições de equilíbrio em cada ponto, ou seja, se é estável, instável ou indiferente.
Se uma partícula de massa for deixada na condição de equilíbrio estável com velocidade de , ela realiza um movimento periódico? Justifique.
Ver solução completaQuestão 9
Considere um potencial, descrevendo uma força conservativa, dado pela função:
- Faça o gráfico da função potencial e da força associada a este potencial, indicando os pontos de máximo e mínimos locais, os pontos que e , e os valores assintóticos para os limites de e
- Desejamos empregar este potencial para aprisionar uma partícula de massa M. Qual é a velocidade máxima da partícula, em x = 0, para que a mesma fique confinada no potencial?
- Para uma partícula com velocidade , vinda de A, podemos realizar o aprisionamento adicionando uma força dissipativa: na região entre , a partícula sofre pequenas variações de momento , opostas ao seu deslocamento, a um intervalo médio (muito menor que o tempo de voo nesta região), resultando em uma força de atrito constante se sua velocidade não for nula. Qual a velocidade máxima de aprisionamento da partícula em função dos parâmetros desta armadilha?
Questão 10
Uma partícula de massa executa um movimento unidimensional e possui energia potencial cuja dependência com a coordenada é onde a e b são constantes positivas.
(a) Encontre a expressão da força que atua sobre a partícula como função da posição;
(b) Faça esboços das funções energia potencial e força como funções da posição da partícula.
(c) Encontre a(s) posição(ões) de equilíbrio da partícula sob a ação dessa força e classifique-o(s) de acordo com a estabilidade;
(d) Determine qual(ais) o(s) intervalo(s) de energia mecânica para o(s) qual(is) uma partícula sujeita a essa força possui movimento numa região limitada da reta.
(e) Determine qual(ais) o(s) intervalo(s) de energia mecânica para o(s) qual(is) uma partícula sujeita a essa força pode ser encontrada a distâncias arbitrariamente grandes da origem.
Ver solução completaQuestão 11
A energia potencial de um sistema é dada pela função .
a) Determine a força como uma função de ;
b) Para quais valores de a força é nula?
c) Faça o gráfico de versus ;
d) Faça o gráfico de versus e indique os pontos de equilíbrio estável e instável.
Ver solução completaQuestão 12
A energia potencial de ligação entre átomos de moléculas diatômicas pode ser descrita, dentro de certos limites, pelo gráfico ao lado, dado pela equação
onde é a distância entre os núcleos dos átomos, a e b são constantes. 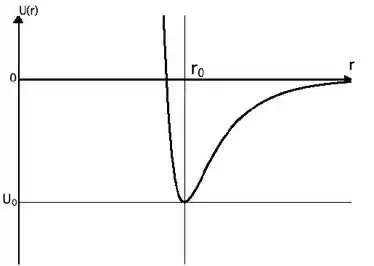
a) Qual a equação da força entre os átomos?
b) Determine a distância de equilíbrio .
c) Determine a energia potencial mínima .
Dê suas respostas somente em termos de e .
Ver solução completaQuestão 13
Uma partícula move-se sob a ação de uma única força conservativa, cuja energia potencial associada está representada na figura abaixo.
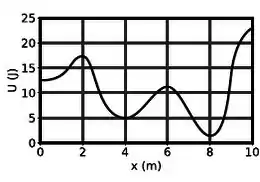
Considerando que num dado instante de tempo a partícula está na posição , com uma energia mecânica total , assinale abaixo a afirmativa que descreve corretamente os pontos de retorno à esquerda e à direita da partícula em metros, respectivamente e :
(a) , e .
(b) , e .
(c) , e .
(d) , e .
(e) indeterminado, e .
(f) indeterminado, e .
(g) Não é possível determinar os pontos de retorno.
Ver solução completaQuestão 14
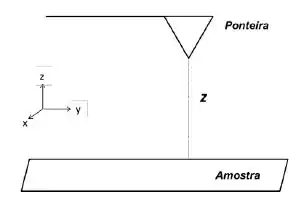
Um aparato bastante utilizado em Nanotecnologia é o microscópio de força atômica, que permite medir a força de interação entre a superfície da ponteira e a superfíce de uma amostra em escala nanométrica. Dentre os modelos usados para descrever essa interação está um variante do potencial Lennard-Jones, conhecido como potencial , cuja forma funcional é dada abaixo:
Onde é a distância entre a ponteira e a amostra, e são parâmetros do potencial, com unidades de energia distância, respectivamente, com e .

Questão 15
Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa , correspondente a um potencial , dado pela figura abaixo. Para este potencial entre as opções abaixo a única incorreta é:
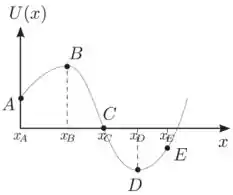
- Na posição a força sobre a partícula é nula;
- Na posição , tem-se a condição de equilíbrio estável;
- No deslocamento do corpo de para o trabalho realizado pela força é positivo;
- O sentido da força na posição é negativo;
- Na posição a força é nula.
Questão 16
Uma partícula que pode-se mover livremente ao longo do eixo tem uma energia potencial da forma
onde e e são constantes positivas. Pode-se dizer que:
A. Nenhuma das opções é certa.
B. Existem vários pontos de equilíbrio estável.
C. Para qualquer valor finito não nulo de , existe uma força que faz que a partícula fique cada vez mais distante de .
D. Se a energia mecânica total é , a energia cinética é mínima em .
E. é um ponto de equilíbrio instável.
Ver solução completaQuestão 17
Considere o movimento unidimensional de uma partícula ao longo do eixo . Tal partícula está submetida a uma única força, e – mostrada na figura – é a função energia potencial associada a esta força. Analise as afirmações abaixo:
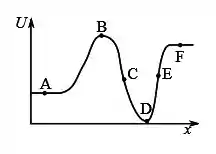
I. A, B e D são pontos de equilíbrio.
II. A partícula irá acelerar no sentido negativo do eixo se estiver no ponto E.
III. B é um ponto de equilíbrio estável.
IV. D é um ponto de equilíbrio estável.
V. D é um ponto de equilíbrio indiferente.
VI. Em C a partícula irá acelerar no sentido negativo do eixo .
Marque a alternativa que contém apenas as VERDADEIRAS.
(a) I, II e III
(b) I, III e V
(c) I, II e V
(d) I, III e IV
(e) I, IV e V
(f) II, IV e V
(g) I, II e IV
(h) III, IV e V
(i) I, IV e VI
(j) II, III e VI
Ver solução completaQuestão 18
Considere a curva de energia potencial, figura 2, , entre duas partículas e , onde é a distância entre elas. Marque a alternativa incorreta:
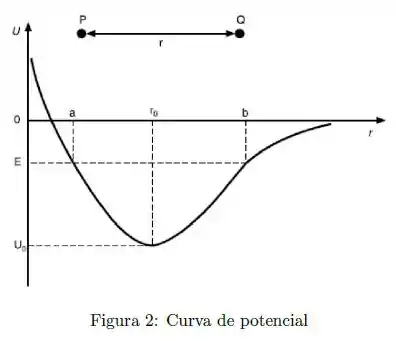
(A) O ponto de equilíbrio vale .
(B) O ponto de equilíbrio é estável.
(C) Se a energia mecânica total for igual a , a distância das partículas oscila em torno de .
(D) Se a energia mecânica total for igual a , existem dois pontos de retorno: e .
(E) Se a energia mecânica total for maior que zero, existirá apenas um ponto de retorno.
Ver solução completaQuestão 19
Uma partícula de massa move-se em uma dimensão ao longo do eixo e de acordo com a energia potencial, em , dada por:
a) Esboce o gráfico de , para
b) Encontre a força associada a esta energia potencial
c) Ache a(s) posição(ões) de equilíbrio, e identifique-o(s) como instável, estável ou indiferente. Justifique sua resposta.
d) Qual é o valor de no ponto de equilíbrio instável?
e) Supondo que a partícula esteja inicialmente em repouso no ponto de equilíbrio estável de , qual é a mínima velocidade que se deve dar a ela para que seu movimento deixe de ser confinado?
Ver solução completaQuestão 20
Uma partícula se movimenta em uma dimensão sob a influência de uma força resultante conservativa, cuja energia potencial está mostrada na figura.
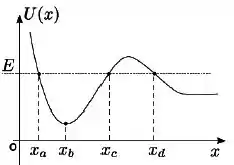
Sabendo que a energia mecânica da partícula é e que inicialmente ela se encontra na posição , é correto afirmar que:
(a) Ela nunca passa pela posição .
(b) é um ponto de equilíbrio estável pois nele a força resultante sobre a partícula é nula.
(c) é um ponto de retorno pois nele a energia cinética é nula.
(d) A energia cinética da partícula é mínima em .
(e) é um ponto de equilíbrio instável pois nele a energia cinética é nula.
(f) A energia cinética da partícula é máxima em .
Ver solução completaQuestão 21
A energia potencial de uma partícula que se move ao longo do eixo é dada por , onde está em joules e em metros. Se a energia mecânica total é os limites de seu movimento são:
(A) ; ;
(B) ; ;
(C) ; ;
(D) ; ;
(E) ; ;
Ver solução completaQuestão 22
Uma partícula se move na direção x sob a ação de uma força cuja energia potencial associada a ela é dada por - b . Quais são os pontos de equilíbrio associados a esta energia potencial?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 24
Uma partícula é lançada em com energia cinética , viajando ao longo do eixo horizontal e submetida a uma forca horizontal cuja energia potencial é conhecida (veja gráfico). A partícula pode se mover somente ao longo do eixo e não existem forças dissipativas.
Assinale a alternativa correta:
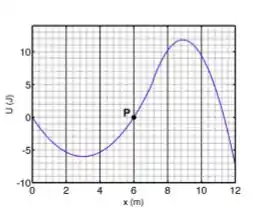
(a) O trabalho necessário para levar a partícula de até só pode ser determinado se conhecermos a massa da partícula.
(b) A energia cinética da partícula no ponto depende do tempo que a partícula permanece no potencial.
(c) A partícula tem energia suficiente para alcançar a posição .
(d) O trabalho necessário para levar a partícula da origem até o ponto de equilíbrio estável é positivo.
(e) O ponto é um ponto de retorno.
(f) A velocidade da partícula em é nula.
(g) A força exercida sobre a partícula no ponto é positiva
Ver solução completaQuestão 25
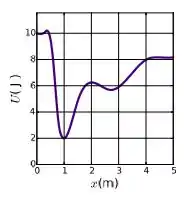
Um objeto se move ao longo do eixo sob a ação de uma forca conservativa. A energia potencial associada a essa força é mostrada na figura ao lado. Sabe-se que é um ponto de retorno. Se é a energia cinética do sistema em e é a componente da forca ao longo da trajetória do objeto no trecho , assinale a alternativa correta:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 26
Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa correspondente a um potencial , dado pela figura abaixo. Para este potencial, entre as opções abaixo, a única incorreta é:
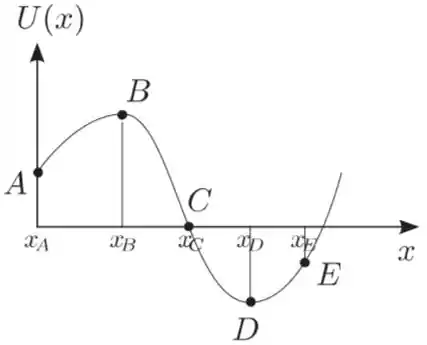
a) na posição a força sobre a partícula é nula;
b) na posição , tem-se a condição de equilíbrio estável;
c) no deslocamento do corpo de para a variação de energia cinética do corpo é positiva;
d) o sentido da força na posição é negativo;
e) na posição a força é nula.
Ver solução completaQuestão 27
O gráfico mostra a energia potencial em função da distância de um objeto em movimento ao longo do eixo x. Em qual dos pontos marcados há um equilíbrio estável?
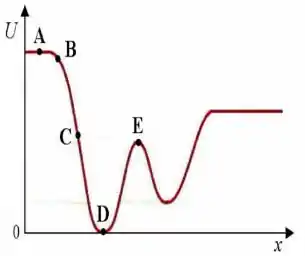
- A
- B
- C
- D
- E
Questão 28
Uma partícula parte do repouso no ponto e se move ao longo do eixo sujeita à energia potencial mostrada no gráfico.
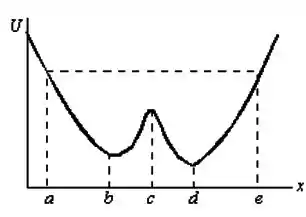
Qual (ou quais) da(s) afirmativa(s) abaixo está(estão) correta(s)?
– A rapidez da partícula é zero em e aumenta à medida que ela se desloca de a
– Os pontos e são pontos de equilíbrio estável
– Em , a energia cinética é máxima.
(a) e
(b) e
(c) e
(d)
(e)
Ver solução completaQuestão 29
A figura mostra a energia potencial de uma partícula que move-se ao longo do eixo sob a ação da força resultante associada a . A alternativa FALSA é
(a) Na posição , tem-se a condição de equilíbrio estável;
(b) No deslocamento da partícula da posição para a posição , o trabalho realizado sobre a partícula é positivo;
(c) O sentido da força na posição é positivo;
(d) Na posição , a força sobre a partícula é nula;
(e) No deslocamento da partícula da posição para a posição , a variação da energia cinética é positiva.
Questão 30
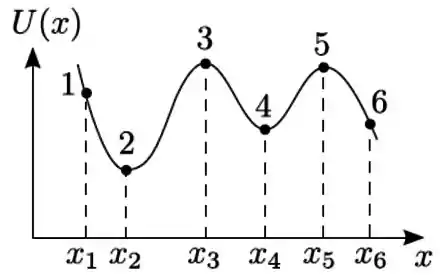
A figura mostra a energia potencial simétrica de uma partícula que se move ao longo do eixo x sob a ação da força resultante associada a . A partícula se encontra confinada neste potencial e possui energia total , também representada no mesmo gráfico. Assinale a afirmação FALSA
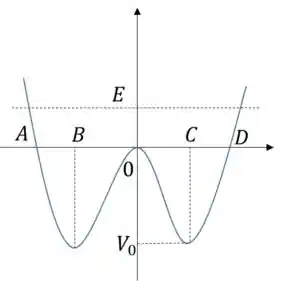
- a partícula fica em repouso ao passar pelo ponto x = 0
(b) o módulo da velocidade é máximo quando a partícula passa pelos pontos B e C
(c) o movimento da partícula não está limitado entre os pontos A e D
(d) a força F é nula apenas nos pontos B, C e x = 0
(e) o ponto C corresponde a um ponto de equilíbrio estável
Ver solução completaQuestão 31
Uma partícula desloca-se ao longo do eixo sob a ação de uma força conservativa , correspondente a uma energia potencial , dada pelo gráfico da figura, na qual o ponto é um ponto de máximo e é um ponto de mínimo. Para esse potencial, entre as opções abaixo a única incorreta é
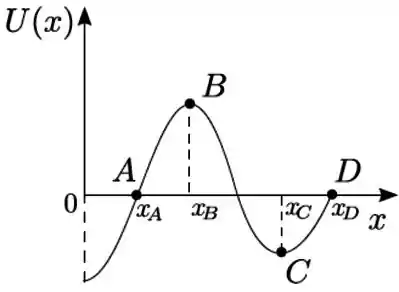
(a) na posição a força sobre a partícula é nula;
(b) na posição , tem-se a condição de equilíbrio estável;
(c) o sentido da força na posição é positivo;
(d) no deslocamento do corpo de para o trabalho realizado pela força é positivo;
(e) na posição a força é nula.
Ver solução completaQuestão 32
Uma partícula se desloca ao longo do eixo sujeita à energia potencial mostrada na figura. Sabendo que é um ponto de retorno. Qual é a energia cinética da partícula em ?
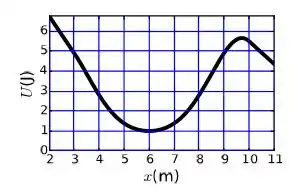
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 33
Uma partícula desloca-se ao longo do eixo , de unitario , sob ação de uma força conservativa , correspondente ao potencial , dado pelo gráfico da figura. Para este potencial, entre as alternativas abaixo, a única INCORRETA é
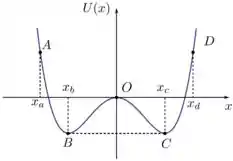
- Na posição a força sobre a particula é nula;
- Nas posições e tem-se a condição de equilíbrio estável;
- No deslocamento da particular de para o trabalho realizado pela força é negativo;
- No deslocamento da partícula de para a variação da energia cinética é ;
- Na posição o sentido da força é positivo.
