Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.Problemas Adicionais - Ex. 64
As capacitâncias dos quatro capacitores da Fig. 25-52 são expressas em termos de uma constante . (a) Se , qual é a capacitância equivalente entre os pontos A e B? (Sugestão: imagine primeiro que uma bateria foi ligada entre os dois pontos; em seguida, reduza o circuito a uma capacitância equivalente.) (b) Responda à mesma pergunta do item (a) para os pontos A e D.
Passo 1
Vamos olhar para o circuito da Fig. 25-52, esquecendo primeiramente o ponto D. Os capacitores 6C e 4C, estão ligados em série, assim podemos achar uma capacitância equivalente entre eles.
Agora podemos redesenhar o circuito:
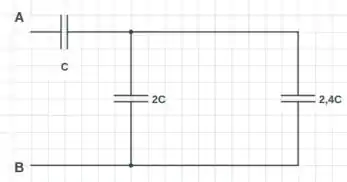Podemos ver, que temos o C em série com os capacitores 2,4 C e 2C que estão em paralelo:
Resolvendo primeiramente os em paralelo:
E finalmente:
Passo 2
No item (b), vamos esquecer o ponto B, na figura 25-52. Sendo assim, podemos ver que o capacitor esta em série com o , assim:
Agora, o circuito fica na forma:
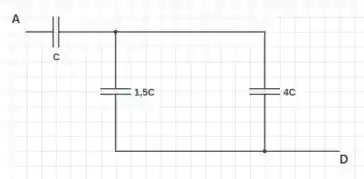
Por ultimo
Resposta
(a)
(b)