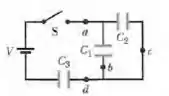
Os capacitares da Fig. Abaixo estão inicialmente descarregados. As capacitâncias são , e e a diferença do potencial da bateria é . Quando a chave S é fechada, quantos elétrons passam (a) pelo ponto a; (b) pelo ponto b; (c) pelo ponto c; (d) pelo ponto d? Na figura, os elétrons estão se movendo para cima ou para baixo ao passarem (e) pelo ponto b; (f) pelo ponto c?

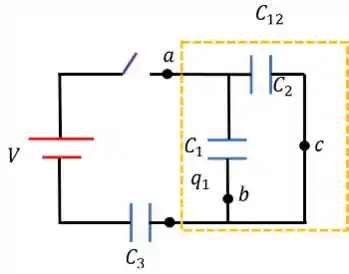
No circuito a seguir, precisamos encontrar o número de elétrons que passam pelos pontos a, b, c e d.

Precisamos encontrar as cargas em cada um dos capacitores e, em seguida, determinar o número de elétrons. Os capacitores estão em paralelo; a capacitância equivalente desses dois capacitores é . O capacitor está em série com :

E

Substituindo :

Porém como a capacitância e estão em serie estão em série a carga em ambos são iguais , então:

A tensão nos capacitores 1 e 2 são as mesmas, pois estão em paralelo:

E a carga total do capacitor é :

Substituindo:

Porém :

Item (a)

A carga que passa pelo ponto a é Se dividirmos essa carga por , obteremos a quantidade de elétrons, que se movem em direção do terminal positivo da bateria.

Item (b)

A capacitância equivalente de e é , a tensão no capacitor 1, que é a mesma tensão no capacitor 2, é . Então, a carga armazenada em é Dividindo por obtemos elétron que passam pelo ponto b, em direção ao capacitor 1.

Item (c)

A carga armazenada em é Dividindo por , obtemos o número de elétrons , que passam em c, em direção ao capacitor 2.

Item (d)

Como o capacitor 3 está em série com a bateria, e com a associação dos capacitores 1 e 2, então o número de elétrons que passam pelo capacitor 3 nada mais é do que a soma de e calculados anteriormente.

elétron que passam no ponto d, em direção aos capacitores 1 e 2.

Item (e)

A corrente move-se do polo positivo para o polo negativo da bateria, como mostrado na figura. A corrente no ponto b está indo para baixo, e como os elétrons se movem na direção oposta da corrente, os elétrons no ponto b estão se movendo para cima.

Item (f)

A corrente move-se do polo positivo para o polo negativo da bateria, conforme mostrado na figura. A corrente no ponto b está indo para baixo, e como os elétrons se movem na direção oposta da corrente, os elétrons no ponto b estão se movendo para cima.

Da mesma forma, os elétrons no ponto c estão se movendo para cima.