Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 25.Problemas Adicionais - Ex. 73
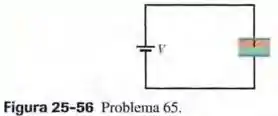
Na Fig. 25-56, as placas do capacitor de placas paralelas têm uma área de e o espaço entre as placas é preenchido por dois blocos de material isolante com de espessura cada um. A constante dielétrica de um dos materiais é e a do outro é . Qual é a carga armazenada no capacitar por uma bateria de ?
Passo 1
Fala aí! Tudo certinho? 😬
Temos um capacitor de placas paralelas com área , preenchidos por dois blocos de espessura , cada um. Sabemos que as constantes dielétricas são e .
Para descobrir a capacitância desse capacitor, podemos considerar que ele é formado por dois capacitores menores ligados em paralelo.
As áreas dos capacitores menores são iguais a do capacitor completo, porém a distância entre as placas é a espessura dos dielétricos.
Assim, utilizando a fórmula para capacitores de placas paralelas com dielétricos, temos que:
Sacou? Bora começar! 😉
Passo 2
Agora, para calcular a capacitância de capacitores em série:
A formula, para a capacitância de um capacitor de placas paralelas é :
assim,
Para encontrar a carga armazenada em um capacitor, podemos utilizar a fórmula:
E aí! Entendeu tudo? Responde Aí! 😁
