Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 50
Um capacitor esférico é composto de uma esfera interna que tem raio e carga , e uma fina casca esférica concêntrica que tem raio , e carga .
(a) Determine o campo elétrico e a densidade de energia como função de , onde é a distância ao centro da esfera, para .
(b) Calcule a energia associada com o campo eletrostático em uma casca esférica entre os condutores que tem raio , espessura e volume .
(c) Integre sua expressão para a Parte (b) para determinar a energia total e compare seu resultado com o obtido usando .
Passo 1
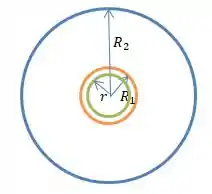
Acho que a primeira coisa a se fazer aqui é desenhar essas duas cascas esféricas concêntricas, não é verdade?
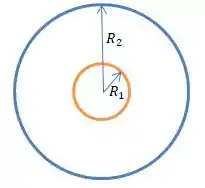
Então, para resolver esses problemas, vamos supor que exista uma carga na esfera laranja e uma carga na esfera de raio azul. Beleza?
Passo 2
Cara... Podemos encontrar o campo elétrico em todas as regiões do espaço pela lei de Gauss, que nos fala que o fluxo de campo elétrico em uma superfície fechada (Gaussiana que a gente deve escolher) é...
Mas aqui temos três regiões distintas, veja...
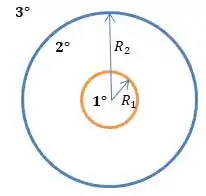
A Gaussiana que vamos escolher serão esferas de raio , de modo que na região...
Na segunda região...
E na terceira uma Gaussiana...
E a Gaussiana que vamos escolher vai ser assim...
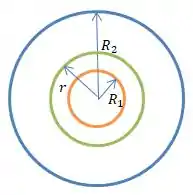
Passo 3
De acordo com a Lei de Gauss...
Onde o fluxo , pelo fato de ser o campo elétrico de uma esfera sempre na direção radial (perpendicular a Gaussiana também esférica), então o fluxo pode ser dado pelo produto...
Onde é a área da Gaussiana: por ser uma Gaussiana esférica de raio , sua área é ...
Agora quem é a carga interna ?
Passo 4
Bem, é aqui que entrará a separação das regiões...
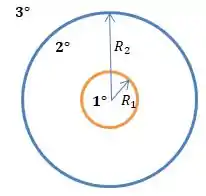
Porque em cada região, a Gaussiana vai ter uma carga interna diferente! Veja bem, supondo a Gaussiana na região ...
Repare que não tem nenhuma carga interna a Gaussiana nessa região, então o campo elétrico para a região será...
Já na segunda região... Quando , a carga que vai estar dentro da Gaussiana vai ser a carga na esfera laranja (), então nesse trecho...
Para a terceira, vamos ter duas cargas presente dentro da Gaussiana: , então na terceira região, o campo elétrico também será nulo...
Passo 5
Sabemos que a energia eletrostática numa região onde se tem campo elétrico é...
Onde é a densidade de energia eletrostática...
No nosso caso, o volume é dado por , então...
Substituindo a expressão do campo elétrico dentro dos condutores...
Passo 6
Integrando essa expressão de até para cobrirmos toda a região que se tem campo elétrico...
E essa é finalmente a energia que está armazenada no interior do capacitor esférico, saca?
Resposta
Letra A:
Letra B:
Letra C: