Exercícios de Capacitância de um Sistema - Lista de Exercícios Resolvida

A figura abaixo representa o processo de descarga de um capacitor como função do tempo. No tempo , a diferença de potencial entre as placas do capacitor era . No instante de tempo , assinalado no gráfico, a diferença de potencial, em volts, entre as placas do capacitor é:

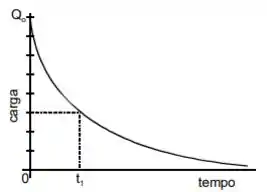
a) b) c) d) e)

Um capacitor tem uma capacitância de . Se o potencial elétrico entre suas placas for , o número de elétrons em excesso na sua placa negativa é (considere a carga de um elétron sendo ):

a) b) c) d) e) Nenhuma das alternativas.

Considere uma esfera condutora maciça de raio que é concêntrica com uma casca esférica condutora de raios interno e externo e respectivamente. A esfera maciça possui carga ao passo que a casca possui carga total . Calcule a capacitância desse sistema.

Considere um cilindro maciço condutor de raio e comprimento que é concêntrico com uma casca cilíndrica condutora de raios interno e externo e respectivamente e de comprimento também. A casca tem densidade linear de carga ao passo que o cilindro tem densidade linear de carga . Calcule a capacitância do sistema.

Um capacitor de placas paralelas tem placas metálicas quadradas de lados com de comprimento, separadas por .

a) Calcule a capacitância deste dispositivo.

b) Quando este capacitor é carregado com , quanta carga é transferida de uma placa para a outra?

Um capacitor é formado por uma esfera condutora de raio e uma casca esférica condutora de raio , conforme a figura.

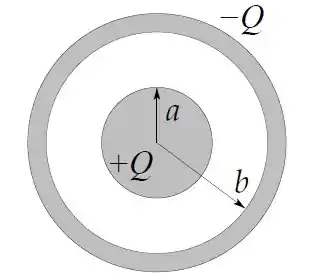
A esfera interna tem carga e a casca esférica tem carga . As respostas devem ser dadas apenas em termos de , , e .

Determine a diferença de potencial entre a esfera interna e a casca esférica.

Calcule a capacitância

Um cilindro condutor de comprimento e raio , com carga , é coaxial a uma camada cilíndrica condutora maior, com raio interno e carga . Despreze efeitos de borda.

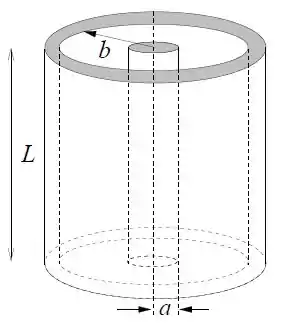
Calcule a capacitância do sistema.

Considere duas placas condutoras circulares de área separadas por uma distância no vácuo, cada uma com densidade de carga constante iguais à e . Suponha que a distância seja desprezível se comparada com as dimensões das placas. Calcule a capacitância desse sistema.

Considere um capacitor de duas placas paralelas (com vácuo entre elas), inicialmente separadas por uma distância e submetidas a uma voltagem . Alguém então dobra a voltagem entre as placas, mantendo a distância de separação.

Conclui-se então que:

A capacitância na nova configuração é o dobro da configuração inicial.

A capacitância na nova configuração é a metade da configuração inicial.

A capacitância na nova configuração é o quádruplo da configuração inicial.

A capacitância não se altera, pois ela é independente da voltagem aplicada.

Nenhuma das afirmativas anteriores está correta.

Sobre capacitores, considere as afirmativas abaixo:

1. A capacitância de um sistema depende da quantidade de carga armazenada em cada condutor.
2. A capacitância de um sistema não depende do tamanho de seus condutores.
3. Quanto maior for a diferença de potencial entre os seus condutores, maior será a capacitância de um sistema.

São VERDADEIRAS as afirmativas:

Um cilindro condutor de comprimento e raio , com carga , é coaxial a uma camada cilíndrica condutora maior, com raio interno e carga . Despreze efeitos de borda.

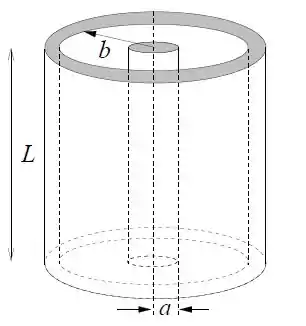
1. Calcule o vetor campo elétrico na região .
2. Calcule a capacitância do sistema.
3. Qual é a energia eletrostática armazenada no sistema?

Um capacitor é formado por uma esfera condutora de raio e uma casca esférica condutora de raio , conforme a figura.

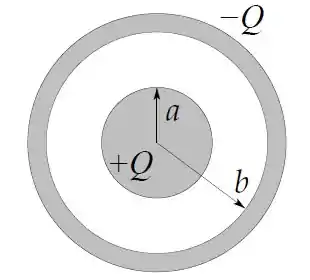
A esfera interna tem carga e a casca esférica tem carga . As respostas devem ser dadas apenas em termos de , , e .

Determine a diferença de potencial entre a esfera interna e a casca esférica.

Calcule a capacitância e determine a energia eletrostática armazenada no capacitor.

. Um capacitor de capacitância é conectado inicialmente a uma bateria e carregado até armazenar uma carga de . A seguir, o capacitor é desconectado da bateria e conectado a dois outros capacitores, inicialmente descarregados, de capacitâncias e , como mostrado na figura abaixo. Nessa situação, as cargas armazenadas nos capacitores e valem, respectivamente:

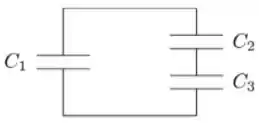
Escolha uma opção:

e

e

e

e

e

e

e

e

Cargas opostas e iguais a são colocadas sobre duas placas quadradas de um capacitor de placas paralelas com ar entre elas. As placas são então separadas a duas vezes a sua distância original, que é pequena em comparação com as dimensões das placas. Qual das seguintes afirmações sobre este capacitor é verdadeira?

A energia armazenada no capacitor permaneceu a mesma.

A densidade de energia no capacitor tem aumentado.

O campo eléctrico entre as placas aumentou.

A diferença de potencial entre as placas duplicou.

A capacitância dobrou.

O capacitor mostrado na figura abaixo está parcialmente preenchido por um material dielétrico de constante dielétrica e está carregado com uma carga . A área do capacitor plano é , a distância entre as placas é e a espessura do dielétrico é . O resto do capacitor encontra-se no vácuo. Determine:

(a) Os vetores campos elétricos nas três regiões no interior do capacitor.

(b) A diferença de potencial entre as placas do capacitor.

(c) A capacitância do capacitor.

Um capacitor cilíndrico é formado por um cilindro condutor de raio e comprimento , com , coaxial a uma casca cilíndrica espessa, também condutora, de raio interno , raio externo e comprimento . A capacitância desse capacitor é dada por:

(a)

(b)

(c)

(d)

(e)

Indique com V se afirmação é verdadeira, ou F, se é falsa

a)_____ Aproxima-se uma partícula carregada de uma esfera condutora e neutra e isolada. Após restabelecido o equilíbrio eletrostático, a força eletrostática resultante sobre a esfera é nula, já que o campo eletrostático em qualquer ponto no interior da esfera é nulo.

b)_____ Um capacitor ideal, originalmente vazio, de placas quadradas, paralelas, tem suas arestas duplicadas, mantendo-se a distância entre as placas constante. Ainda que preenchamos tal capacitor com um material isolante qualquer, é impossível fazer a nova capacitância igual à antiga.

c)_____Em um condutor em equilíbrio eletrostático, o potencial elétrico tem o mesmo valor em todos os pontos de seu interior.

d)_____ Se o fluxo elétrico através de uma superfície fechada for zero, então não há partículas carregadas na região interior à superfície.

e)_____ De acordo com o princípio da superposição, o campo eletrostático criado por um sistema de partículas carregadas em um ponto de uma superfície fechada é dado pela soma vetorial apenas dos campos das cargas que estiverem dentro dessa superfície.

f)_____ O campo eletrostático em qualquer ponto de uma superfície equipotencial tem sempre o mesmo módulo, já que ele é sempre perpendicular a essa superfície.

g)_____ Se um capacitor é mantido isolado enquanto um material dielétrico é inserido em seu interior, sua energia armazenada diminui.

h)_____Um dipolo elétrico, formado por partículas de cargas e , separadas por uma distância fixa , encontra-se em uma região onde há campo eletrostático uniforme . Inicialmente, o seu momento de dipolo aponta na mesma direção e no mesmo sentido que o campo. O dipolo é girado de até ficar antiparalelo ao campo (mesma direção de  , mas sentido oposto). O trabalho realizado pelas forças eletrostáticas sobre o dipolo, nesse processo, foi positivo.

i)_____ Duas linhas de campo elétrico nunca podem se cruzar.

j)_____ A lei de Gauss só é válida para distribuições de carga com algum tipo de simetria.

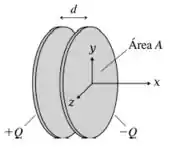
Um capacitor é um dispositivo eletrônico formado por duas placas metálicas idênticas, carregadas com cargas , separadas por um distância conforme ilustrado na figura abaixo.

Capacitores comerciais são construídos com placas cujos diâmetros são muito maiores que a separação e são de grande interesse em aplicações de eletrônica. Considerando esses capacitores comerciais, assinale a opção que melhor descreve o potencial eletrostático entre as placas carregadas .

Um capacitor de placas paralelas de área está conectado a uma bateria cuja diferença de potencial é .

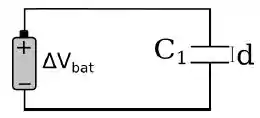
As placas do capacitor estão separadas por uma distância . Sem interromper as conexões, mãos isoladas separam um pouco mais as placas, sendo a nova distância entre elas igual a . A carga na situação inicial e a carga na situação final são, respectivamente.

e

e

e

e

e

(Capítulo 25.3 – Exercício 6) Pretende-se usar duas placas de metal com de área para construir um capacitor de placas paralelas. (a) Qual deve ser a distância entre as placas para que a capacitância do dispositivo seja 1,00 F? (b) O dispositivo é fisicamente viável?

(Capítulo 25.3 – Exercício 5) Qual é a capacitância de uma gota formada pela fusão de duas gotas esféricas de mercúrio com 2,00 mm de raio?

(Capítulo 25.3 – Exercício 3) Um capacitor de placas paralelas possui placas circulares com um raio de 8,20 cm, separadas por uma distância de 1,30 mm. (a) Calcule a capacitância. (b) Qual é a carga das placas se uma diferença de potencial de 120 V é aplicada ao capacitor?

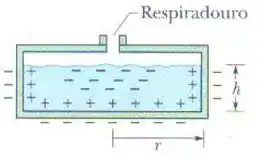
(Cap 25 Ex- 36) Como engenheiro de segurança, o leitor precisa emitir um parecer a respeito da prática de armazenar líquidos condutores inflamáveis em recipientes feitos de material não condutor. A companhia que fornece um certo líquido vem usando um recipiente cilíndrico, feito de plástico, de raio r = 0,20 m, que está cheio até uma altura h = 10 cm, menor que a altura interna do recipiente (figura abaixo). A investigação do leitor revela que, durante o transporte, a superfície externa no recipiente adquire uma densidade de cargas negativas de (aproximadamente uniforme). Como o líquido é um bom condutor de eletricidade, a carga do recipiente faz com que as cargas do líquido se separem.

(a) Qual é a carga negativa induzida no centro do líquido?

(b) Suponha que a capacitância da parte central do líquido em relação à terra seja 35 pF. Qual é a energia potencial associada à carga negativa desse capacitar efetivo?

(c) Se ocorre uma centelha entre a terra e a parte central do líquido (através do respiradouro), a energia potencial pode alimentar a centelha. A energia mínima necessária para inflamar o líquido é 10 mJ. Nessa situação, o líquido pode pegar fogo por causa de uma centelha?

Um capacitor de placas paralelas no vácuo, separadas de , apresenta diferença de potencial entre as placas. Desprezando-se os campos de borda, qual o módulo da densidade de carga em cada uma das placas, em ? E necessário use . Obs: utilize uma casa decimal na sua resposta.

Um capacitor esférico é constituído por duas cascas esféricas metálicas concêntricas de raios a e b com a

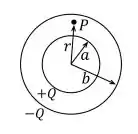
(a) (1,0 ponto) Calcule o vetor campo elétrico em um ponto P, localizado a uma distância r do centro geométrico do capacitor, tal que a

(b) (1,0 ponto) Calcule a diferença de potencial entre as placas do capacitor.

(c) (0,5 ponto) Calcule a capacitância deste capacitor.

1 - Dois capacitores e são associados em paralelo e submetidos à uma determinada diferença de potencial. O capacitor tem:

1. o dobro da carga do capacitor
2. metade da carga do capacitor .
3. o dobro da diferença de potencial à qual está submetido.
4. metade da diferença de potencial à qual está submetido.
5. a mesma carga do capacitor .

(Cap 25 Ex- 37) Um capacitor de placas paralelas, cujas placas têm uma área de e estão separadas por uma distância de 3,00 mm, é carregado por uma bateria de 6,00 V. A bateria é desligada e a distância entre as placas do capacitor é aumentada (sem descarregá-lo) para 8,00 mm. Determine

(a) a diferença de potencial entre as placas;

(b) a energia armazenada pelo capacitor no estado inicial;

(c) a energia armazenada pelo capacitor no estado final;

(d) a energia necessária para separar as placas.

Qual das seguintes afirmativas é FALSA?

a) No processo de carregamento de um capacitor, cria-se um campo elétrico entre suas placas.

b) O trabalho necessário para carregar um capacitor pode ser pensado como sendo o trabalho necessário para criar um campo elétrico entre suas placas.

c) A densidade de energia no espaço entre as placas de um capacitor é diretamente proporcional ao módulo do campo elétrico.

d) A diferença de potencial entre as placas de um capacitor é diretamente proporcional ao módulo do campo elétrico.

e) A capacitância é caracterizada por fatores geométricos do capacitor.

Quando a distância entre as placas paralelas de um capacitor carregado é , a diferença de potencial entre as placas é . Se a distância for reduzida para , a nova diferença de potencial entre as placas será:

a)

b)

c)

d)

e)

Considere um capacitor de placas paralelas separados de uma distância com um dielétrico de permissividade elétrica entre as placas. Como podemos diminuir a capacitância desse capacitor?

1. Resfriando as placas.
2. Aumentando a corrente nos terminais
3. Diminuindo a tensão nos terminais
4. Diminuindo a distância entre as placas
5. Diminuindo a permissividade do meio

Um capacitor de placas paralelas tem uma capacitância . Um segundo capacitor de placas paralelas tem placas com o dobro da área separadas pelo dobro da distância.

A capacitância do segundo capacitor é:

;

;

;

;

;

Considere um capacitor formado por duas placas paralelas quadradas de lado , colocadas a uma distância uma da outra, sendo . Calcule:

A capacitância do capacitor.

As duas placas de um capacitor esférico possuem raios e , com . Considerando que há vácuo entre as placas, e que as placas interna e externa possuem cargas e , respectivamente, calcule:

A diferença de potencial entre as placas

Dois cilindros metálicos, concêntricos, infinitamente longos e de raios e atuam como placas de um capacitor cilíndrico. Considerando que há vácuo entre as placas, e que as placas interna e externa possuem densidade linear de carga e , respectivamente, calcule:

A capacitância de um comprimento de segmento do capacitor.

As duas placas de um capacitor esférico possuem raios e , com . Considerando que há vácuo entre as placas, e que as placas interna e externa possuem cargas e , respectivamente, calcule:

A capacitância do capacitor.

As duas placas de um capacitor esférico possuem raios e , com . Considerando que há vácuo entre as placas, e que as placas interna e externa possuem cargas e , respectivamente, calcule:

A energia armazenada no capacitor.

Dois cilindros metálicos, concêntricos, infinitamente longos e de raios e atuam como placas de um capacitor cilíndrico. Considerando que há vácuo entre as placas, e que as placas interna e externa possuem densidade linear de carga e , respectivamente, calcule:

A energia armazenada em um segmento de comprimento do capacitor.

Refaça todos os itens do problema anterior, considerando agora que a região entre cilindros é preenchida com um material dielétrico de constante dielétrica .

Refaça todos os itens do problema anterior, considerando agora que a região entre as esferas é preenchida com um material dielétrico de constante dielétrica .

8ª questão - Um capacitor de placas paralelas está conectado aos terminais de uma bateria cuja força eletromotriz vale . Após o carregamento do capacitor, e mantendo-se a conexão com a bateria, mãos isoladas afastam as placas. Marque a alternativa FALSA.

A) A diferença de potencial permanece constante entre as placas do capacitor.

B) A carga no capacitor diminui após o afastamento.

C) A capacitância diminui após o afastamento.

D) A energia armazenada no capacitor aumenta após o afastamento.

E) O módulo do campo elétrico entre as placas diminui após o afastamento.