Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 24.1 - Ex. 46

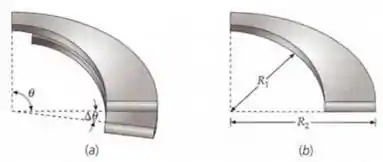
APLICAÇÃO EM ENGENHARIA. Um goniômetro é um instrumento preciso para medida de ângulos. Um goniômetro capacitor está mostrado na Figura 24-40a. Cada placa do capacitor variável (Figura 24-40b) consiste em um semicírculo metálico plano que tem raio interno R 1 e raio externo R 2 . As placas compartilham um eixo de rotação em comum e a largura do espaçamento de ar separando as placas é d . Calcule a capacitância como função do ângulo θ e dos parâmetros dados.

Passo 1

Podemos calcular a capacitância desse treco aí sabendo que a capacitância entre duas placas paralelas e com uma área entre elas sendo A assim...

C = ε 0 A d   →

Só que repare que a área que está entre as placas depende de θ ...

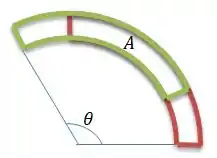
Então bora encontrar essa área aí!

OBS: A área de um pedaço anel circular de ângulo θ é...

A a n e l = θ 2 π π R 2 2 - π R 1 2

Passo 2

Se a gente chamar esse pedacinho de área verde e vermelha de A 1 ...

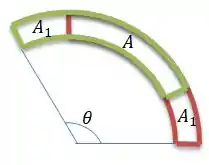
A soma das três áreas vai ser a área do anel...

A + 2 A 1 = θ 2 π π R 2 2 - π R 1 2

Onde θ é um ângulo que varia de π 2 a π , saca?

Agora quem é A 1 ?

Passo 3

Repare que A área apenas do pedaço do anel vermelha é conhecida, isto é...

A v e r m e l h a = 1 4 π R 2 2 - π R 1 2

E essa área vermelha é a junção das áreas...

A v e r m e l h a = A 1 + A   →

A 1 + A = 1 4 π R 2 2 - π R 1 2

Assim, a área A 1 será igual...

A 1 = 1 4 π R 2 2 - π R 1 2 - A

Passo 4

Voltando para a equação do passo 2...

A + 2 A 1 = θ 2 π π R 2 2 - π R 1 2

E substituindo A 1 ...

A + 2 1 4 π R 2 2 - π R 1 2 - A = θ 2 π π R 2 2 - π R 1 2   →

A + 1 2 π R 2 2 - π R 1 2 - 2 A = θ 2 π π R 2 2 - π R 1 2   →

1 2 π R 2 2 - π R 1 2 - A = θ 2 π π R 2 2 - π R 1 2   →

1 2 π R 2 2 - π R 1 2 - θ 2 π π R 2 2 - π R 1 2 = A  

Podemos simplificar se quisermos...

A = 1 2 π R 2 2 - π R 1 2   1 - θ π

Então, a capacitância em função de θ vai ser...

C = ε 0 A d   →

C = ε 0 π 2 d R 2 2 - R 1 2   1 - θ π  

Resposta

C = ε 0 π 2 d R 2 2 - R 1 2   1 - θ π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitor de placas paralelas, de capacitância igual a 200p F e placas separadas de 1,00m m , tem uma diferença de potencial de 50V entre as placas. Calcule a força entre as placas.
Um capacitor de placas paralelas tem capacitância de 200p F e o volume contido entre as placas é de 100c m 3 . Calcule:a) a diferença de potencial entre as placas se o capacitor possui uma carga de 3,
Um capacitor cilíndrico possui as seguintes características: comprimento igual a 10c m , raio da placa interna igual a 1,0c m e raio da placa externa igual a 2,0c m . Calcule:a) a sua capacitância;b)
Considere duas cascas esféricas condutoras concêntricas, de raios R 1 e R 2R 1 .a) Calcule os coeficientes de potencial P 11 , P 22 , P 12 e P 21 e verifique que P 12 = P 21 .b) Mostre que C - 1 = P 1
A energia potencial acumulada no circuito visto na Figura 17.15 é V 0 e o capacitor da direita está descarregado. Calcule a energia potencial V f após a chave ser fechada e as correntes cessarem.