Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 118
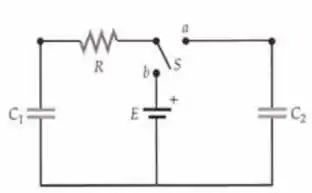
Os capacitores e estão conectados a um resistor de resistência R e a uma bateria ideal que tem tensão nos terminais , como mostra a Figura 25-79. A chave S está inicialmente no contato a e ambos os capacitores estão descarregados. A chave é, então, girada para o contato b e deixada lá por um longo tempo. Finalmente, no instante t=0, a chave retorna ao contato a.
a) Compare quantitativamente a energia total armazenada nos dois capacitores em t=0 e em um longo tempo depois.
b) Determine a corrente através de R como uma função de t para t > 0.
c) Determine a energia entregue ao resistor como uma função de t para t > 0.
d) Determine a energia total dissipada no resistor depois de t = 0 e compare-a com a perda da energia armazenada determinada na parte (a).
Passo 1
a)
Meus queridos e minhas queridas, a questão é um pouco extensa, então, vamos com calma!
As equações das energias final e inicial são:
Visto que:
Então:
Isolando :
Lembrando que:
Vamos substituir as equações encontradas nas equações iniciais:
Vamos fazer duas comparações:
- Primeiro, a diferença entre o potencial inicial e o final:
- Segundo, a razão entre o potencial inicial e o final:
O que significa que já que o fator .
Passo 2
b)
Vamos aplicar a lei de Kirchoff para quando a chave está em a:
Onde:
Então:
Vamos aplicar a conservação da carga durante o carregamento:
Vamos substituir na equação original:
Vamos admitir que a solução da EDO é dada por:
Com isso, teremos:
Por comparação:
E
Simplificando por :
Lembrem:
Logo:
Por fim, vamos derivar a equação encontrada em função de t:
Como:
Finalmente:
Passo 3
c)
Vamos encontrar a equação da energia dissipada em função do tempo:
Passo 4
d)
Agora, para encontrarmos a energia total dissipada, precisamos resolver a seguinte integral:
Como:
Teremos: