Enunciado
Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 26.Exercícios - Ex. 79
Um capacitor, inicialmente descarregado, é conectado em série a um resistor e a uma fonte de fem E 110 V, que possui resistência interna desprezível. Imediatamente após a conexão do circuito, a corrente através do resistor é de 6,5 105 A. A constante de tempo para o circuito é 5,2 s. Determine a resistência do resistor e a capacitância do capacitor
Passo 1
E aiii galera!
Tudo bom com vocês?
Vamos fazer mais uma questãozinha?
Abaixo temos o esquema do circuito:
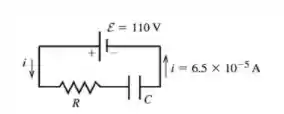
Inicialmente, a carga do capacitor é zero, então por a tensão no capacitor é zero.
Pela lei das malhas temos:
Passo 2
A constante de tempo é:
Então,
A resistência é grande, então a corrente inicial é pequena e a constante de tempo é grande.
Resposta
Exercícios de Livros Relacionados
Os capacitores C 1 e C 2 estão conectados a um resistor de resistência R e a uma bateria ideal que tem tensão nos terminais V 0 , como mostra a Figura 25-79. A chave S está inicialmente no contato a e
(a) Dar apoio à afirmação de que um condensador com fugas (para o qual a resistência do dielétrico é finita) pode ser modelado como um condensador que tem uma resistência infinita em paralelo com uma
A figura 25-77 mostra a base do circuito de varrimento utilizado num osciloscópio. O interruptor S é um interruptor electrónico que fecha sempre que o potencial através do interruptor S aumenta para u
No circuito mostrado na Figura 25-78, R 1 = 2,00M Ω , R 2 = 5,00M Ω , e C = 1,00μ F . O capacitor está inicialmente sem carga em ambas as placas. Em t= 0, a chave S é fechada e, em t= 2,00 s, a chave
O capacitor na Figura 25-49 está inicialmente descarregado. A chave S está fechada e permanece fechada por um longo tempo. Durante este tempo, (a) a energia fornecida pela bateria é 1 2 C ε 2 , (b) a