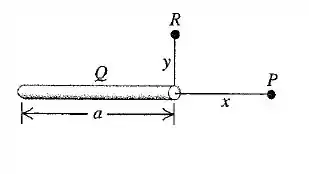
Uma carga elétrica total é uniformemente distribuída ao longo de uma barra fina, de comprimento. Considere o potencial igual a zero no infinito. Calcule o potencial nos seguintes pontos (veja a figura):

(a) No ponto, a uma distância à direita da barra.

(b) no ponto, a uma distância acima da extremidade direita da barra.

(c) Como se reduzem os resultados da parte (a) e da parte (b) quando ou se tornam maiores do que?

letra a)

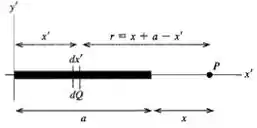
Sabemos que é a distância da distribuição de carga até o ponto onde quero calcular o potencial.

Se considerarmos o desenho abaixo, temos:

Substituindo na integral:

Essa integral vai nos dar

letra b)

Agora, para o iremos considerar esse novo desenho abaixo, onde será a hipotenusa do triângulo de lados e

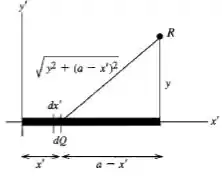
Então se usarmos Pitágoras:

Substituindo na integral vamos ter:

Vamos fazer uma substituição simples:

Trocando os limites de integração

Temos então:

Para resolver a integral iremos colocar o em evidência:

Agora podemos fazer uma substituição:

Mas por que essa substituição?????

Identidade trigonométrica!

Temos agora na integral:

E essa integral é tabelada!!!!

Precisamos agora voltar para a variável .

Além disso temos:

Então:

Nosso potencial será então:

letra c)

Queremos agora saber o que acontece com os potenciais quando e

Para o item (a):

Precisamos agora expandir o :

Para ,

Nosso potencial fica:

Para muito grande, nosso potencial se torna o potencial de uma carga puntiforme.

Para o item (b):

Expandindo o termo da raiz:

O termo ao quadrado irá embora porque

Então

E como vimos no passo anterior, podemos expandir o .

Temos então:

Para grande, o potencial também se aproxima ao potencial de uma carga puntiforme.