Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 2.Problemas - Ex. 4
Uma carga negativa fica em equilíbrio quando colocada no ponto médio do segmento de reta
que une duas cargas positivas idênticas. Mostre que essa posição de equilíbrio é estável para
pequenos deslocamentos da carga negativa em direções perpendiculares ao segmento, mas que é instável para pequenos deslocamentos ao longo dele.
Passo 1
Vamos lá! Vamos desenhar a situação
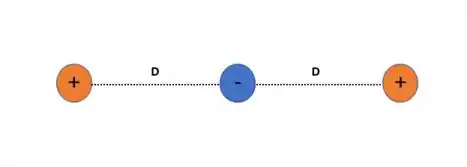
Agora vamos colocar as forças que estão atuando
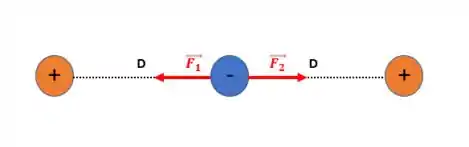
A força resultante é a somatório das forças
As forças que atuam são forças eletrostáticas e de mesmo módulo
Então, a força resultante é nula, pois as distâncias entre as duas cargas é a mesma e as cargas positivas são idênticas. Assim temos que a carga negativa permanece em equilíbrio nessa situação.
Passo 2
Agora vamos pro primeiro caso, se houver um pequeno deslocamento da carga negativa na direção perpendicular ao segmento
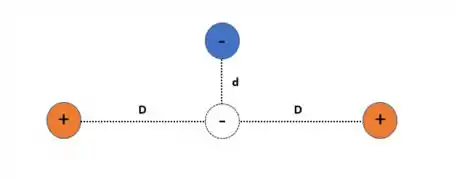
Vamos colocar as forças que atuam sobre a carga negativa
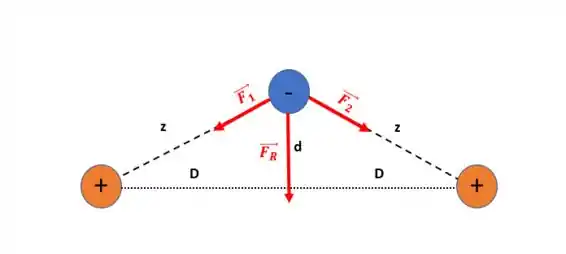
Agora a carga negativa está a uma distância das cargas positivas. Temos a força na direção horizontal vão se cancelar e a força resultante será para baixo. De forma que busca voltar à posição de equilíbrio.
Passo 3
No segundo caso temos um pequeno deslocamento na direção do segmento
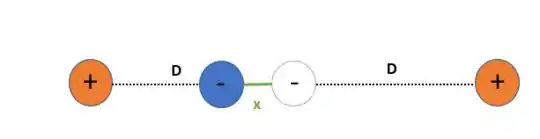
As forças que atuam são
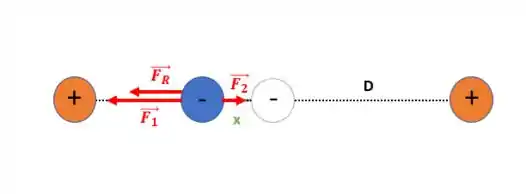
Como a distância entre a carga negativa e carga positiva da esquerda diminui com um valor , temos que a sua força terá módulo:
Já com a carga à direita a força diminui, pois a distância aumenta em . A Força terá módulo:
Como quanto menor o denominador maior o resultado Assim a força resultante será para a direita, criando uma instabilidade no sistema independe qual seja o deslocamento nessa direção.
Resposta
Ei, a resposta está no passo a passo :)