Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 21.1 - Ex. 73

Uma carga puntiforme de - 3,00   μ C está localizada na origem; uma carga puntiforme de 4,00   μ C está no eixo x em x = 0,200   m ; uma terceira carga puntiforme Q está localizada no eixo x em x = 0,320   m . A força elétrica na carga de 4,00   μ C é de 240   N no sentido de + x . (a) Determine a carga Q . (b) Com esta configuração de três cargas, em que posição ou posições o campo elétrico é nulo?

Passo 1

A figura seguinte representa a configuração de cargas.

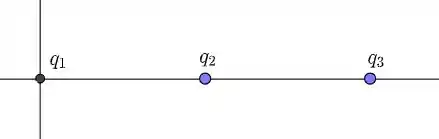
Notemos que q 1 atrai q 2 , de modo que há uma força orientada em - x . Porém, como a força em q 2 está orientada em + x (conforme diz o enunciado), segue que q 3 deve atrair q 2 ; ou seja q 3 < 0 . Assim, segue que

F 23 - F 21 = F r e s u l t a n t e k q 2 Q d 23 2 - k q 2 q 1 d 12 2 = F r e s u l t a n t e 9 × 10 9 4 × 10 - 6 - Q 0,120 2 - 9 × 10 9 3 × 10 - 6 4 × 10 - 6 0,2 2 = 240

Resolvendo para Q , temos

Q = - 9,71 × 10 - 5   C

Passo 2

(b) Vamos dividir a figura em quatro regiões, conforme mostra a figura a seguir:

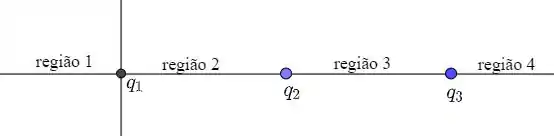
  1. Região 1:

    2. Temos que

    E → = k q 1 d 1 2 i ^ - q 2 d 2 2 i ^ + q 3 d 3 2 i ^ E → = k 3,00 × 10 - 6 x 2 - 4 × 10 - 6 x + 0,200 2 + 97,1 × 10 - 6 x + 0,320 2 i ^

    Para que E → = 0 nessa região, devemos ter:

    3 x 2 - 4 x + 0,200 2 + 97,1 x + 0,320 2 = 0

    Devemos usar uma calculadora (ou um software) para resolver essa equação. Veremos que tal equação não possui nenhuma raiz com x < 0 (restrição para pertencer à região 1). Sendo assim, nenhum ponto dessa região possui campo elétrico nulo.

  2. Região 2:

    3. Temos que

    E → = k - q 1 d 1 2 i ^ - q 2 d 2 2 i ^ + q 3 d 3 2 E → = 10 - 6 k - 3 x 2 - 4 x - 0,200 2 + 97,2 x - 0,320 2

    Para que E → = 0 , devemos ter

    - 3 x 2 - 4 x - 0,200 2 + 97,2 x - 0,320 2 = 0

    Usando uma calculadora, vemos que as únicas raízes possíveis são x = 0,169   m e x = 0,0508   m .

  3. Região 3:

    4. E → = k - q 1 d 1 2 i ^ + q 2 d 2 2 i ^ + q 3 d 3 2 i ^ E → = 10 - 6 k - 3 x 2 + 4 x - 0,200 2 + 97,2 x - 0,320 2 = 0

    Assim, temos que

    - 3 x 2 + 4 x - 0,200 2 + 97,2 x - 0,320 2 = 0

    Resolvendo essa equação com o auxílio de uma calculadora, vemos que não há nenhuma raiz.

  4. Região 4:

E → = k - q 1 d 1 2 i ^ + q 2 d 2 2 - q 3 d 3 2 E → = 10 - 6 k - 3 x 2 + 4 x - 0,200 2 + 97,2 x - 0,320 2 = 0

Resolvendo a equação com o auxílio de uma calculadora, vemos que não há nenhuma raiz.

Resposta

  1. Q = - 97,2   μ C
  2. x = 0,0508   m ou x = 0,169   m .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A carga pontiforme q 1=-5,00n C está na origem e a carga puntiforme q 2=+3,00n C está no eixo x em x=3c m . O ponto P está no eixo y em y=4c m .Calcule os campos elétricos E 1 e E 2 no ponto P produzi
Uma carga puntiforme de +8,75μ C está colada em uma mesa horizontal com atrito desprezível. Ela está atada a uma carga puntiforme de -6,5μ C por um por um fio leve, não condutor, de 2,5c m . Um campo
Campo elétrico no núcleo, A distância entre os prótons do núcleo é da ordem de 10 - 15m( 1m f ) . Qual é o módulo do campo elétrico produzido por um próton a uma distância de 1,5f m dele?Como esse cam
Um elétron se desloca no sentido de leste para oeste em um campo elétrico uniforme de 1,50 N/C, que aponta do oeste para o leste. No ponto A, a velocidade do elétron é 4,5x10 5 m / s no sentido do oes
Duas cargas puntiformes q são colocadas sobre o eixo O x , uma no ponto x = a e outra no ponto x = - a . Determine o módulo, a direção e o sentido do campo elétrico no ponto x=0 . Deduza uma expressão