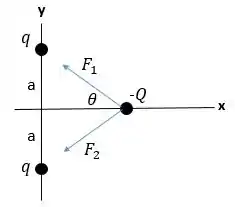
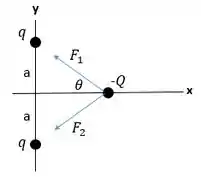
Duas cargas puntiformes positivas estão localizadas sobre o eixo sobre os ponto e . Uma carga puntiforme negativa está localizada sobre algum ponto do eixo .
- Faça um diagrama do corpo livre mostrando as forças que atuam sobre a carga .
- Determine as componentes e da força resultante da ação das cargas e sobre . (Sua resposta deve envolver somente e a coordenada da terceira carga).
- Qual é a força resultante sobre a carga quando ela está na origem ?
- Faça um gráfico da componente da força resultante sobre em função de para valores de compreendidos entre
Passo 1
Fala galera! Tudo bem? Bora resolver essa questão de eletrostática? Para o item a), podemos usar a Lei de Coulomb para calcularmos as forças entre as cargas nas posições indicadas e a carga . Consideraremos o seguinte: é a força exercida pela carga , em . é a força exercida pela carga , em . Agora repara: ambas são feitas sobre a carga ! A distância entre cada carga e a carga pode ser determinada tirando uma relação de pitágoras:
O ângulo formado entre a horizontal e a reta que passa entre as cargas analisadas é dado por:
Essas relações ficam evidentes analisando a imagem abaixo. Podemos traças o diagrama de corpo livre justamente desenhando as forças que estão atuando sobre a carga da seguinte maneira:
Passo 2
Para o item b), quando temos , terão componentes horizontais no sentido . Assim, teremos, para o eixo :
Nesse caso, consideramos como sendo a força resultante na força em .
Como vimos, temos que:
Substituindo na nossa relação, teremos:
Simplificando a expressão ficamos com:
Com isso, teremos:
Para a direção , temos a resultante como:
Dessa forma, temos:
Por essa expressão, se a gente olhar com cuidado, podemos ver que nem precisamos saber qual o valor de ! Repare que as duas quantidades que estamos diminuindo são de mesma intensidades. Ou seja, essa diferença será zero!
Para , terão, agora. componentes horizontais no sentido . Assim como fizemos antes, teremos, para o eixo :
Esse resultado é análogo ao que obtivemos antes, considerando a direção ! Podemos simplificar nosso trabalho apenas trocando o sinal da resultante anterior. Ou podemos realizar as contas pra verificar isso:
Nosso valor de , relembrando:
Substituindo na expressão, fica:
Simplificando um pouco, temos:
Logo:
Da mesma forma que, para , teremos uma resultante nula, justamente por conta da simetria do problema, não alteramos a localização de , nesse segundo momento, em , mas apenas em .
Assim, a força resultante na vertical será:
Passo 3
Para o item c), a força resultante sobre a carga quando ela dá quando ela está na origem será a soma das forças que cada carga realiza nela. Dessa forma, teremos a seguinte situação:
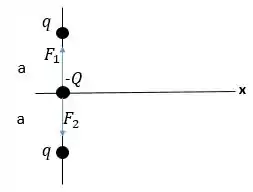
Pra simplificar, a nossa carga será nossa carga 3, como anteriormente. Assim, a força resultante sobre ela será:
Mas repare que os sentidos das forças serão contrários e que elas estão sob a mesma distância. Além disso, as cargas terão mesmo módulo. Intuitivamente, havaliamos que a força resultante é nula! Mas, as contas podem confirmar essa intuição:
Substituindo as informações:
Da mesma maneira que em não haverá forças:
Com isso:
Passo 4
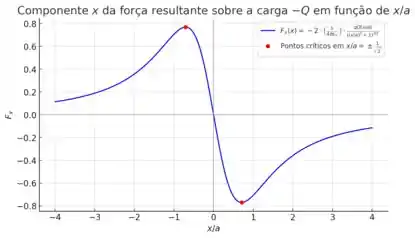
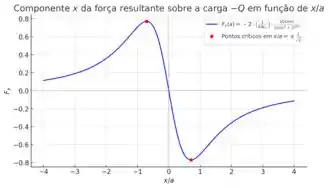
Para o item d), o gráfico pode ser obtido avaliando a força resultando em . Vamos analisar a expressão que obtemos no item a):
Essa expressão relaciona justamente a força resultante sobre a partícula de caraga com a sua posição em relativa as outras duas cargas . Se a gente reparar bem, podemos reescrever a expressão como sendo:
O primeiro termo se torna justamente um constante, já que ele não depende do valor de . Podemos obter o esboço do gráfico analisando as derivadas dessa função. Pra isso, aplicaremos a derivada com relação à . Nesse caso, vamos precisar aplicar a regra do quociente das derivadas, que é:
Com isso, temos:
Precisamos aplicar uma pequena regra da cadeia. Organizando os termos, ficamos com:
Se a gente analisar com cuidado, podemos encontrar o máximo dessa função, avaliando onde essa derivada será nula. Com isso:
Para que a derivada seja nula, o numerador dessa última relação que encontramos deve ser nulo:
Organizando o termo, temos:
Para que essa expressão seja nula, temos dois casos possíveis. Ou teremos:
Que resulta em:
O que não apresenta solução real!
Para a segunda possibilidade, temos que:
Que, simplificando, fica:
Ou seja:
Simplificando a equação, sobra pra gente que:
Encontramos os pontos onde a função é máxima, ou seja, onde a força resultante sobre é nula!! Seria o análogo a dizer que, nesse ponto, a partícula se encontra em equilíbrio. Agora, se tomarmos valores, de forma que:
Podemos ver que:
Sendo assim, valores menores que esse, resulta em uma derivada positiva!
Da mesma forma que:
Nos resulta em valores:
Ou seja, a derivada aqui é negativa!!!
Vamos organizar o que obtemos:
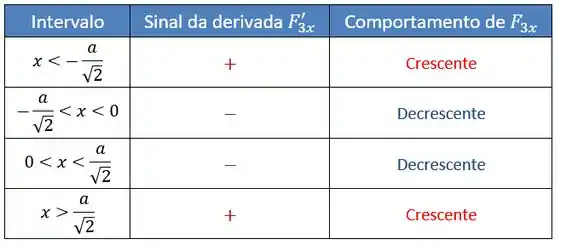
O esboço do gráfico ficaria assim: