Uma carga puntiforme positiva q está localizada sobre o eixo no ponto e uma carga puntiforme positiva está localizada sobre o eixo no ponto Uma carga puntiforme negativa está localizada em um ponto em algum ponto sobre o eixo .
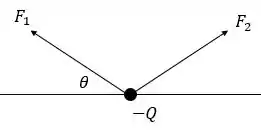
- Faça um diagrama do corpo livre mostrando as forças que atuam sobre a carga .
- Determine os componentes x e y da força resultante da ação das cargas e sobre . (Sua resposta deve envolver somente e a coordenada x da terceira carga).
- Qual é a força resultante sobre a carga quando ela dá quando ela está na origem ?
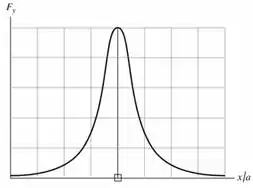
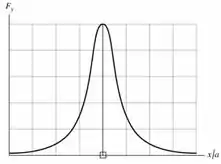
- Faça um gráfico da componente da força resultante sobre em função de para valores de compreendidos entre
Passo 1
- As forças que atuam sobre será representado no diagrama do corpo livre a seguir.
- Como não temos valores para determinados dados, força resultante estará em função de e a coordenada x da terceira carga. Sendo assim,
- Quando carga esta na origem a força resultante y será,
- Faça um gráfico da componente da força resultante sobre em função de para valores de compreendidos entre
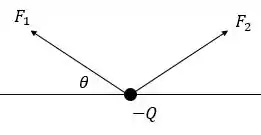
Aravés da relação trigonométrica podemos analisar a distância entre as cargas e e e .
Passo 2
Passo 3
Passo 4