Enunciado
Física - Young and Freedman - Vol 2- Ed: 14º - Capítulo 12.Exercícios - Ex. 3
Um casal de astronautas concorda em se encontrar no espaço depois do horário de trabalho. O plano deles é deixar que a gravidade os aproxime. Um deles tem uma massa de 65 kg e o outro, de 72 kg, e eles partem do repouso afastados por 20,0 m um do outro. (a) Desenhe um diagrama do corpo livre de cada astronauta e use-o para descobrir sua aceleração inicial. Como uma aproximação bruta, podemos modelar os astronautas como esferas uniformes. (b) Se a aceleração dos astronautas permanecesse constante, quantos dias eles teriam de esperar antes que um alcance o outro? (Cuidado! Ambos possuem aceleração em direção ao outro.) (c) Sua aceleração realmente permaneceria constante? Se não, ela aumentaria ou diminuiria? Por quê?
Passo 1
Faaaaala meu povo, bora iniciar mais um livrinho com a gente!
Para essa questão, primeiramente iremos definir o primeiro astronauta com massa e o segundo com . Ambos os astronautas se movem com uma aceleração devido à força gravitacional entre ambos, essa força é dada pela lei geral da gravidade de Newton descrita como:
Onde é a distância entre os dois astronautas e é dada por e é a constante geral da gravidade e é igual a . Assim temos que:
Passo 2
Letra a)
Essa força é exercida sobre cada astronauta e faz com que ele se mova com uma aceleração. Pela lei do movimento de Newton, essa aceleração pode ser encontrada por:
Isolando aceleração, temos:
Assim, sabendo o valor da força, iremos substituir a massa de cada astronauta e dessa forma calcular sua aceleração.
A força gravitacional entre os dois os aproxima, então o diagrama de corpo livre é mostrado na figura abaixo:
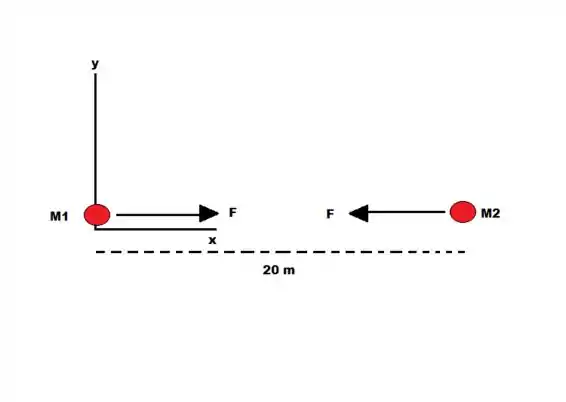
Passo 3
Letra b)
Como mostram nossos resultados na letra (a), a aceleração é muito pequena para ambos os astronautas, então faz sentido que demore dias para atingir os outros. Para determinar o tempo, usamos equações de movimento na forma:
Onde é a distância que a pessoa percorre, é o tempo e é a velocidade inicial. Temos que considerar a velocidade e distância de cada astronauta de forma que teremos então a seguinte equação:
Sabemos que o valor das distâncias , reorganizando a equação, temos:
Agora a gente vai substituir os valores:
Passo 4
Letra c)
A força gravitacional entre ambos é dada pela equação:
Como mostrado por esta equação, a força muda conforme a distância entre as duas massas muda. Ambos os astronautas se aproximam, o que significa que a distância entre eles diminui. Nesse caso, a força entre os dois aumenta, portanto, a aceleração de cada um aumenta.
Tudo certinho? Te vejo na próximaaaaa!
Resposta
Letra a)
Letra b)
Letra c)