Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 45

Uma casca esférica não condutora de raio interno R 1 e raio externo R 2 tem densidade volumétrica uniforme de carga ρ . (a) Determine a carga total na casca. (b) Determine expressões para o campo elétrico em todas as regiões.

Passo 1

Fala ai galera. Essa questão está pedindo para a gente determinar o campo elétrico em todas as regiões em uma esfera não condutora. Para isso, vamos usar a lei de Gauss tomando como superfície gaussiana uma esfera, beleza?

Passo 2

  1. Como a densidade é constante, podemos simplesmente calcular a carga fazendo o produto da densidade vezes o volume da esfera.

    2. O volume da esfera é:

    V = 4 3 π R 2 3 - R 1 3

    Assim, temos que

    q = ρ V = 4 3 π ρ R 2 3 - R 1 3

    Passo 3

  2. Vamos dividir em várias regiões. Temos que:
  • Para r < R 1 :

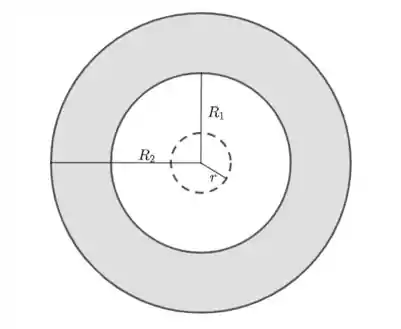
    • Nesse caso, q i n t = 0 . Assim,

    ∮ E   d A = q i n t ε 0 = 0 ∴ E = 0

  • Para R 1 < r < R 2 , temos

    • q i n t = ρ ⋅ V ' q i n t = 4 3 π ρ r 3 - R 1 3

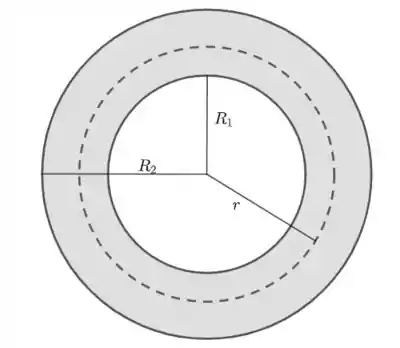
    Assim, segue que

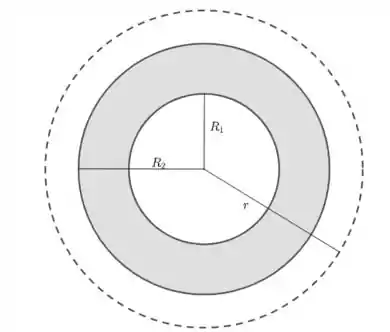
    ∮ E   d A = q i n t ε 0 E 4 π r 2 = 4 3 π ρ r 3 - R 1 3 ε 0 E = ρ r 3 - R 1 3 3 ε 0 r 2

  • Para r > R 2

    • Temos que

    q i n t = q

    Dessa forma,

    ∮ E   d A = q ε 0 E 4 π r 2 = 4 3 π ρ R 2 3 - R 1 3 ε 0 E = π ρ R 2 3 - R 1 3 3 ε 0 r 2

    Resposta

  1. 4 3 π ρ R 2 3 - R 1 3
  • Para r < R 1 , E = 0 ;
  • Para R 1 < r < R 2 , E = ρ r 3 - R 1 3 3 ε 0 r 2
  • Para r > R 2 , E = π ρ R 2 3 - R 1 3 3 ε 0 r 2

    • Resposta

    Ei, a resposta está no passo a passo :)

    Ver Outros Exercícios desse livro

    Exercícios de Livros Relacionados

    A figura ex28.1 mostra as secções transversais de dois cilindros coaxiais infinitamente longos. O cilindro interno possui uma carga positiva, e o cilindro externo, uma carga negativa de mesmo valor ab
    A figura ex28.3 mostra as secções transversais de dois planos infinitos carregados e paralelos. Desenhe a figura sobre um pedaço de papel e, depois, desenhe sobre ela os vetores do campo elétrico de m
    Qual é o fluxo elétrico resultante através do toróide (i.e., a superfície com a forma de um “pneu”) da FIGURA EX28.20?
    A figura ex28.2 mostra as secções transversais de duas esferas concêntricas. A esfera interna possui uma carga negativa. A esfera exterior possui uma carga positiva de maior valor absoluto do que o da
    A Terra cria um campo elétrico vertical à sua superfície, orientado para baixo e com uma intensidade média de 100N / C . Este campo é gerado através de vários processos atmosféricos, incluindo os raio