Enunciado
Física - Randall D. Knight - Eletricidade e Magnetismo- Ed: 2º - Capítulo 28.Exercícios e Problemas - Ex. 41
A Terra cria um campo elétrico vertical à sua superfície, orientado para baixo e com uma intensidade média de . Este campo é gerado através de vários processos atmosféricos, incluindo os raios. Qual é o excesso de carga sobre a superfície da Terra?
Passo 1
Faaaaaala, galera... Tranquileba??
Assumiremos a Terra como um formato esférico perfeitamente simétrica, para que assim possamos assumir, como argumento de simetria, a lei de fluxo elétrico de gauss.
Assim, fazendo um desenho para ilustrar, temos:
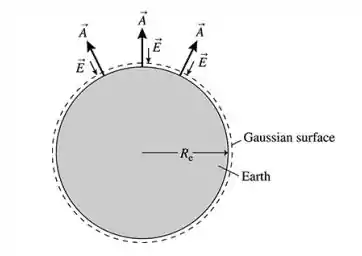
E a área de uma esfera é dada por:
E assumindo o raio da Terra como:
Assim:
Passo 2
Sabemos também que apara uma carga interna em uma superfície fechada
E sabendo que permissividade elétrica no vácuo é
Passo 3
Assim:
Resposta
Exercícios de Livros Relacionados
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Para seu projeto no Ensino Médio, você está projetando um tubo Geiger para detecção de radiação no laboratório de física nuclear. Este instrumento consistirá em um tubo longo metálico cilíndrico que t
No Problema 46, considere que radiação ionizante produza um íon e um elétron a uma distância de 1,50c m do longo eixo do fio central do tubo Geiger. Suponha que o fio seja positivamente carregado e te
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Uma casca esférica não condutora de raio interno R 1 e raio externo R 2 tem densidade volumétrica uniforme de carga ρ . (a) Determine a carga total na casca. (b) Determine expressões para o campo elét