Enunciado
Física - Moysés - Vol. 3- Ed: 1º - Capítulo 4.Problemas - Ex. 10
Uma casca hemisférica de raio está uniformemente carregada com carga positiva de densidade superficial .
- Ache o potencial no ponto central . (Tomando )
- Uma partícula de massa e carga positiva é colocada no ponto e largada a partir do repouso. A que velocidade a partícula tenderá quando se afastar muito de .
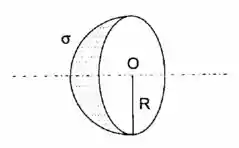
Passo 1
Se liga! Vamos definir o elemento na superfície como
Podemos lembrar que
Passo 2
Podemos calcular o potencial como
Passo 3
Podemos achar a velocidade pedida no item (b), através da conservação da energia.
Nesse caso, a energia potencial é dada por
Lembrando que a energia cinética é
Podemos escrever que
Resposta
Exercícios de Livros Relacionados
Qual é a diferença de potencial V34 na FIGURA EX30.16?
A FIGURA P29.65 mostra duas esferas uniformemente carregadas. Qual é a diferença de potencial entre os pontos a e b? Que ponto se encontra a um potencial mais alto? Dica: Em qualquer ponto, o potencia
Duas gotas esféricas de mercúrio são, cada uma, dotadas de uma carga de 0.10 nC e de um potencial de 300 V. As duas gotas se fundem formando uma única gota. Qual é o potencial na superfície da nova go
Dado que a superfície de um condutor com carga é equipotencial, isso significa que a carga está uniformemente distribuída?
Vimos que no interior de um condutor oco estamos protegidos dos campos das cargas externas. Se estivermos do lado de fora de um condutor oco que contenha cargas, estaremos protegidos dos campos criado