Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 18.3 - Ex. 20
Em um certo experimento , uma pequena fonte radioativa deve se mover com velocidades selecionadas, extremamente baixas. O movimento é conseguido prendendo a fonte a uma das extremidades de uma barra de alumínio e aquecendo a região central da barra de forma controlada. Se a parte aquecida da barra da figura tem um comprimento a que taxa constante a temperatura da barra deve variar para que a fonte se mova com uma velocidade constante de ?
Passo 1
Vamos olhar o desenho:
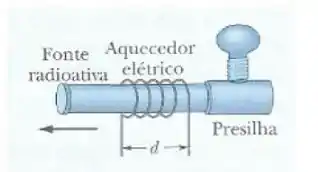
O movimento da fonte pode ser relacionado com quanto ela expande (por conta do aumento de temperatura) em um determinado tempo e podemos relacionar essa quantidade com a velocidade que o problema fornece.
Passo 2
Para determinar recorremos a fórmula da expansão linear:
Dividimos os dois lados da equação pela variação de tempo , assim surge do lado esquerdo a velocidade e do lado direito a taxa com que a temperatura varia no tempo:
Passo 3
Agora basta substituir os valores: (lembrando que o coeficiente de expansão linear do alumínio pode ser encontrado no livro texto)
Resolvendo temos: