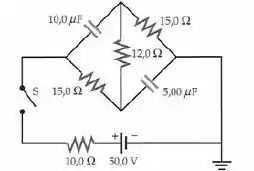
A chave S mostrada na figura abaixo é fechada depois de ter permanecida aberta por um longo tempo. (a) Qual é o valor inicial da corrente na bateria logo aos a chave S ter sido fechada? (b) Qual é a corrente na bateria depois de um longo tempo após a chave ter sido fechada? (c) Quais são as cargas nas placas dos capacitores depois de um longo tempo após a chave ter sido fechada? (d) A chave S é reaberta. Quais são as cargas nas placas dos capacitores depois de um longo tempo após a chave S ter sido reaberta?
Passo 1
FALAAA GALERA, tudo de buenas? i hope so! Vamos pensar um poquito sobre como vamos resolver essa questão...hum...acompanhe-me.
1) Quando a chave está fechada a diferença de potencial entre os capacitores é zero (pois eles não possuem cargas) e os resistores na parte da ponte do circuito (o meio) estão em paralelo;
2)Quando um longo período de tempo passa, a corrente através dos capacitores será zero e os resistores estarão em série.
Nos dois casos, se aplicássemos a Segunda Lei de Kirchhoff’s no circuito todo, obteremos a corrente total. Para encontramos as cargas finais nos capacitores, podemos usar a definição de capacitância e aplicar a Segunda Lei de Kirchhoff’s nas malhas que contem dois resistores e um capacitor para encontrar a diferença de potencial entre os capacitores!
ATENÇÃO! ATENÇÃO! Se você não sabe acerca das Leis de Kirchhoff’s ou sobre a definição de capacitância recomenda que vá ler alguns resumos disponíveis aqui no responde aí :D! Depois volta pra essa questão, pra ter um entendimento melhor e não surtar da cabeça! SEM MAIS DELONGAS! VAMOS PARA AS ALTERNATIVAS!
Passo 2
Para a alternativa (a), aplicaremos a Segunda Lei de Kirchhoff’s no circuito logo após que a chave é fechada (lembrando que representa a resistência equivalente dos resistores da ponte):
Com isto, basta achar a resistência equivalente dos resistores na ponte:
Substituindo:
Agora vamos para a alternativa (b).
Passo 3
Na alternativa (b), aplicaremos a Segunda Lei de Kirchhoff’s no circuito quando um longo período de tempo passa após a chave ter sido fechada (lembrando que representa a resistência equivalente dos resistores da ponte):
Com isto, basta achar a resistência equivalente dos resistores na ponte:
Substituindo:
Agora vamos para a alternativa (c).
Passo 4
Para a alternativa (c) basta usar a definição de capacitância para os dois capacitores em termos das suas diferenças de potencial finais:
Agora aplicaremos a Segunda Lei de Kirchhoff’s na malha contendo o capacitor de e os resistores de e , para encontrarmos a diferença de potencial do capacitor de :
Agora aplicaremos a Segunda Lei de Kirchhoff’s na malha contendo o capacitor de e os resistores de e , para encontrarmos a diferença de potencial do capacitor de :
Substituindo na definição de capacitância, temos:
TERMINAMOS A ALTERNATIVA (c), agora, vamos para a última!
Passo 5
Na alternativa (d), queridos gafanhotos, as cargas nas placas do capacitor após um longo tempo em que a chave S é reaberta serão iguais a zero, pois não passará mais corrente, logo, não haverá cargas.
Resposta
a)
a)
a) e
d) As cargas presentes no capacitor serão iguais a zero