Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 26.Exercício - Ex. 45
No circuito indicado na Figura 26.59, cada capacitor possui carga inicial de modulo igual a 3,50 nC em suas placas. Após a chave S ser fechada, qual será a corrente no circuito no instante em que os capacitores tiverem perdido da energia inicial armazenada?
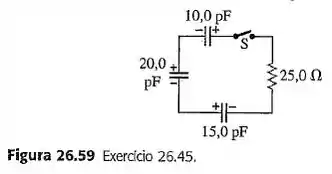
Passo 1
A energia armazenada é proporcional ao quadrado da carga no capacitor; portanto, ela obedecerá a uma equação exponencial, mas não a mesma equação da carga.
A energia armazenada no capacitor é
e a carga nas placas é
A corrente é
Passo 2
Assim,
Quando o capacitor perde de sua energia armazenada, a energia é da energia inicial, que é .
Nos dá que:
Neste momento, a corrente é
Então,
Passo 3
Quando a energia é reduzida em , nem a corrente nem a carga são reduzidas nesse percentual.
Resposta
Exercícios de Livros Relacionados
A chave S mostrada na figura abaixo é fechada depois de ter permanecida aberta por um longo tempo. (a) Qual é o valor inicial da corrente na bateria logo aos a chave S ter sido fechada? (b) Qual é a c
Uma carga constante de 1,00m C está na placa carregada positivamente do capacitor de 5,00μ F mostrado na figura abaixo. Determine (a) a corrente na bateria e (b) as resistências R 1 ,R 2 , R 3 .
Em t = 0 o interruptor na Figura abaixo é girado para o contato b depois de ter estado no contato a por um longo tempo. (a) Determine a energia armazenada no capacitor depois de o interruptor ter sido
No circuito da Figura abaixo, C = 0 ,120μ F e ℇ = 100 Vℇ . A chave é girada para o contato b depois de ter estado no contato a por um longo tempo, e 4.00 s depois, a diferença de potencial no capacito
Para o circuito mostrado na Figura abaixo, C = 6,00μ F , ℇ = 100 Vℇ e R = 500 Ω . Depois de ter estado em contato com a por um longo tempo, o interruptor é girado para o contato com b. (a) Qual é a ca