Enunciado
Física - Tipler - Vol 2- Ed: 6º - Capítulo 25.1 - Ex. 95
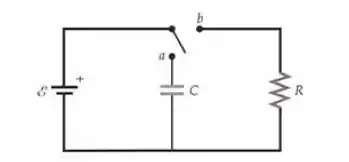
Para o circuito mostrado na Figura abaixo, , e . Depois de ter estado em contato com a por um longo tempo, o interruptor é girado para o contato com b. (a) Qual é a carga na placa superior do capacitor logo após o movimento do interruptor para o contato a? (b) Qual é a corrente inicial logo após o movimento do interruptor para o contato a? (c) Qual é a constante de tempo deste circuito? (d) Quanta carga está na placa superior do capacitor depois de o interruptor ser girado para o contato b?
Passo 1
FALA GALERA, TUDO BEM COM VCS? Espero que sim, agora vem comigo, que é sucesso. Essa questão é baseada puramente em aplicação de equações, podemos usar a definição de capacitância para achar a carga inicial no capacitor e a Lei de ohm para achar a corrente inicial do circuito, podemos encontrar a constante de tempo usando sua definição e a carga no capacitor depois de usando a carga como uma função do tempo. Se liga nas equações que usaremos:
(1)
(2)
(3)
(4)
Estabelecido isso, simbora para as alternativas!
Passo 2
Para a alternativa (a), basta usar a equação 1 e substituir os termos pelos dados estabelecidos na questão:
Faremos o mesmo processo para as demais alternativas; Para a alternativa (b), usaremos a equação 2:
Para a alternativa (c), usaremos a equação 3:
Para a alternativa (d), usaremos a equação 4, utilizando os dados da questão e o resultado da equação 1 e 3:
Resolvemos a questão, prego na tampa do caixão (até rimou), até a próxima galera!
Resposta
a)
b)
c)
d)