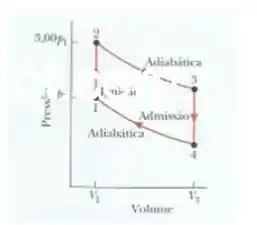
O ciclo da figura abaixo representa a operação de um motor de combustão interna a gasolina. O volume . Suponha que a mistura de admissão gasolina-ar é um gás ideal com . Qual é a razão , , , , ? Qual é a eficiência do motor?

(b) Agora para o processo adiabático descrito por temos essa relação válida:

Do gráfico tiramos as seguintes informações:

• ;

E do passo sabemos que a razão entre é .

Então, se nosso objetivo é calcular saca só esse “truque sujo”: vou dividir a equação ali em cima por e você vai que que vai surgir o que queremos:

Massa né? Isso vai ser feito nos próximos passos para determinar as outras razões que o problema pede ;)

Voltando para nossa expressão, ela pode ser simplificada assim:

Agora vamos substituir os valores dos volumes retirados do gráfico e que :

(c) Para determinar a razão vamos usar a expressão para um processo adiabático envolvendo volume e temperatura:

Do gráfico temos que , então basta substituir na expressão acima e cancelar os termos em comum no lado direito:

(d) Para determinar a razão entre as pressões e vamos proceder de maneira similar ao passo . Vamos analizar o processo . Ele é adiabático, certo? Então a relação entre pressão e volume é dada por:

O que queremos é a razão que envolve , então fazendo o mesmo “truque sujo” de dividir por temos:

Agora do gráfico tiramos os valores de pressão e volume:

• ;
• ;

E temos também que , assim a razão entre as pressões e é dada por:

Podemos simplificar e isolar do lado esquerdo:

(e)Agora para determinar a razão entre as pressões e , sabemos que o processo que envolve esses estados é adiabático, então a relação entre pressão e volume é:

Do gráfico temos que , assim é só substituir:

Assim a razão entre as pressões é:

(f)Por fim, o problema pede a eficiência da máquina.

Para isso precisamos dos valores de calor da fonte quente e da fonte fria.

Sabemos que nos processos adiabáticos não há troca de calor. Sendo assim, o calor da fonte quente vai ser dado pelo processo que é a volume contante.

O calor da fonte fria também vai ser dado pela expressão do calor molar a volume constante, mas entre os estados e :

Mas daí você se pergunta “e as temperaturas?? E agora?” Calma! O que queremos é a eficiência, e ela é proporcional à razão . Olha lá pra expressão da fonte quente. Ela não envolve ? E nós não acabamos de calcular a razão entre as diversas temperaturas? Então calma que existe luz no fim do túnel!

O valor da eficiência vai ser dado por:

Olha aí o que falei! Temos a razão entre as temperaturas e ! Assim a eficiência vaiser dada por: