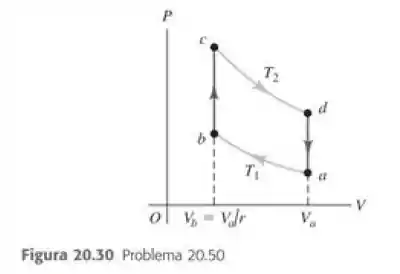
O Ciclo de Stirling é semelhante ao ciclo Otto, a não ser pelo fato de que a compressão e a expansão do gás ocorrerem isotermicamente e não adiabaticamente, como no ciclo Otto. O ciclo Stiling é usado em uma máquina de combustão externa (na verdade, queimar o combustível não é necessário; qualquer forma de produzir uma diferença de temperatura serve –gradiente solar, geométrico, de temperatura do oceano etc.), o que significa que o gás dentro do cilindro não é usado no processo de combustão. O calor é fornecido continuamente pelo fluido combustível no exterior do cilindro , em vez de vir de uma explosão no interior do cilindro como no ciclo Otto. Por essa razão, as máquinas que funcionam com o ciclo Stirling são mais silenciosas do que as máquinas que funcionam com o ciclo Otto, uma vez que não existe válvula de admissão nem vávular de exaustão (a principal fonte de ruído do motor). Embora pequenas máquinas de Striling possam ser usadas em diversas aplicações, o uso do ciclo Stirling em um automóvel não teve êxito porque o motor é maior, mais pesado e mais caro do que o motor convencional do automóvel. No ciclo, o fluido de trabalho realiza as seguintes etapas (Figura 20.20):

(i)Compressão isotérmica à temperatura do estado inicial até o estado , com uma razão de compressão .

(ii)Aquecimento a volume constante até o estado com temperatura .

(iii)Expansão isotérmica à temperatura até o estado .

(iv)Esfriamento a volume constante retonando para o estado inicial .

Suponha que o fluido de trabalho moles de um gás ideal (para qual não depende da temperatura). a) Calcule e nas etapas e não envolvem fontes de calor externas, mas usam a regeneração: a mesma substancia que transfere calor ao gás dentro do cilindro na etapa absorve calor de volta do gás na etaá . Portanto, os calores transferidos e não desempenham papel na determinação da eficiência da máquina. Explique essa ultima afirmação comparando as expressões de e obtidas na parte (a). c) Calcule a eficiência de um ciclo Stirling em termos da temperatura e . Como ele se compara com a eficiência de um ciclo de Carnot operando entre essas mesmas temperaturas? (Históricamente o cilco Stirling foi deduzido antres do ciclo de Carnot.) Esse resultado viola a segunda lei da termodinâmica? Explqie. Infelizmente a máquina que funciona com o ciclo Stirling não pode atingir essa eficiência devido a problemas nos processos de transferência de calor e perdas de pressão na máquina.

Passo 1

Passo 2

Passo 3

Resposta