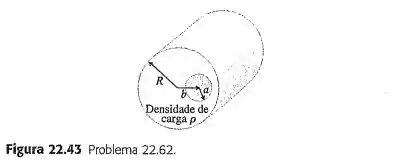
Um cilindro isolante muito longo, de raio , possui um buraco cilíndrico, com raio , perfurado ao longo de toda a extensão do eixo paralelo ao eixo do cilindro. O eixo do buraco está a uma distância do eixo do cilindro, em que (Figura ). A parte maciça do cilindro possui uma densidade volumétrica de carga uniforme . Encontre o módulo, a direção e o sentido do campo elétrico no interior do buraco e mostre que é uniforme em todos os pontos do volume do buraco. (Sugestão: Veja o Problema .)

Como sabemos, o campo elétrico no centro do cilindro é nulo devido ao fato do seu valor depender da distância entre um determinado ponto até o seu centro. Pensando nisso, podemos considerar o cilindro isolante com raio e densidade volumétrica e dizer que o buraco seria outra esfera, porém com densidade e localizada em , visto que nesse caso o campo elétrico é nulo em .

Dessa forma, o campo no interior do buraco será dado pela soma dos campos dos dois cilindros consideradas. Então:

Portanto:

Um detalhe para ficarmos atentos é o fato de que, como o campo elétrico não depende da distância , então o campo é uniforme em toda a região do interior do buraco e a sua direção e sentido são definidos pelo vetor .