Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.4 - Ex. 6

Na Fig. 23-28, uma rede para pegar borboletas está imersa em um campo elétrico uniforme de módulo E = 3,0 m N/C. O plano do aro da rede, uma circunferência de raio a = 11 cm, é mantido perpendicular à direção do campo. A rede é eletricamente neutra. Determine o fluxo elétrico através da rede.

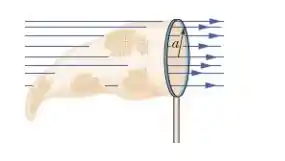
Passo 1

Temos o seguinte, uma rede circular, de raio a   =   11   c m , está em uma região de campo elétrico E   =   3,0   m N / C . Precisamos determinar o fluxo elétrico através da rede. Vamos fazer um desenho pra visualizar isso.

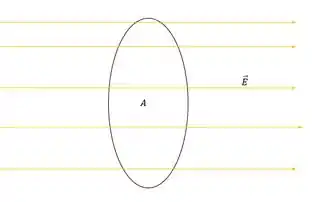
Para calcular o fluxo do campo através da rede é só a gente calcular a área da rede e aplicar a equação do fluxo:

Φ → = E → ⋅ A →

Passo 2

Precisamos calcular a área do aro da rede, mas antes vamos dar uma melhorada no nosso produto escalar, já que ele pode ser escrito assim:

Φ = E A c o s ( θ )

Onde θ é o ângulo entre os vetores. E aqui a gente precisa analisar pra onde aponta o vetor área:

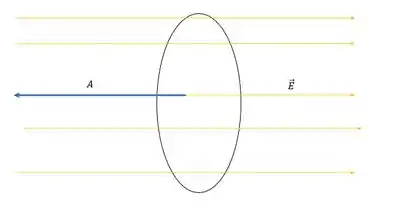
Como a rede tá pra esquerda, o seu vetor área está nesse sentido, portanto podemos dizer aqui que:

θ = 180 °

Φ = E A c o s 180 = - E A

Vamos então calcular essa bendita área:

A = π a 2 = π 11 × 10 - 2 2 = 38,01 × 10 - 3 m 2

E agora com a área vamos substituir todo mundo na equação do fluxo com E = 3 m N / C

Φ = - 3,0 × 10 - 3 38,01 × 10 - 3 = - 1,14 × 10 - 4 N m ² / C

Resposta

Φ = - 1,14 × 10 - 4 N m ² / C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A F i g .25 - 42 é uma seção de uma barra condutora de raio R 1=1,30m m e comprimentoL=11,0m no interior de uma casca coaxial, de paredes finas, de raio R 2=10,0 R 1 e mesmo comprimento L . A carga da
Uma placa metálica quadrada, de 8,0c m de lado e espessura insignificante, possui uma carga total de 6,0×10 - 6C . (a) Estime o valor do módulo E do campo elétrico perto do centro da placa (a 0,50m m
A Fig. 25 - 47 mostra as seções retas de duas placas de grande extensão, paralelas, isolantes,positivamente carregadas, ambas com uma distribuição superficial de carga σ=1,77×10 - 22C / m ² ². Determi
Na F i g .25 - 48 a , um elétron é arremessado verticalmente para cima, com uma velocidade v s=2,0×10 5m / s , a partir das vizinhanças de uma placa uniformemente carregada. A placa é isolante e muito
A Fig. 25 - 36 mostra duas cascas esféricas isolantes mantidas fixas no lugar. A casca 1 possui uma densidade superficial de carga uniforme de + 6,0μ C / m ² ² na superfície externa e um raio de 3,0c