Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 23.4 - Ex. 4

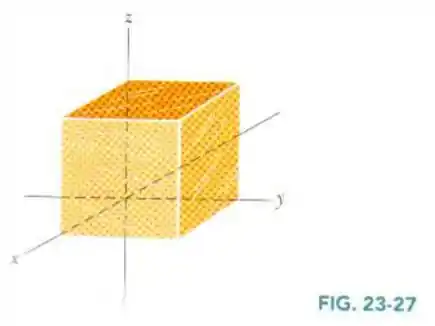
Em todos os pontos da superfície do cubo da Fig. 23-27, o campo elétrico é paralelo ao eixo z. O cubo tem 3,0 m de aresta. Na face superior do cubo, E = - 34 k ^ N / C ; na face inferior, Ê = + 20 k ^ N / C . Determine a carga que existe no interior do cubo.

Passo 1

Olá, meu nobre. Yuri aqui e vou te ajudar a resolver essa atividade.

Bem, vamos entender a situação, esse cubo de 3,0m de aresta, tem um campo elétrico paralelo ao eixo Z. E sabemos que a face superior do cubo tem campo   E = - 34 k ^ N / C e a face inferior Ê = + 20 k ^ N / C .

Como o campo elétrico é paralelo ao eixo Z, só vamos ter fluxo elétrico nas faces superiores e inferiores. Agora é tranquilo, pois só precisamos somar o fluxo dessas duas faces e podemos aplicar o teorema de Gauss.

Passo 2

Para calcular o fluxo em uma face, basta usar a fórmula:

Φ = E → ⋅ A →

Temos que nos atentar para o sinal do fluxo, pois temos que usar que o fluxo para dentro do cubo é negativo, assim:

Φ s u p e r i o r = ( - 34 k ^ ) ∙ 3,0 2

= - 306   k ^   N ∙ m 2 C

Agora para a face inferior

Φ i n f e r i o r = ( - 20   k ^ ) ∙ 3,0 2

= - 180 k ^   N ∙ m 2 C

Somando os fluxos:

Φ = - 180 - 306 = - 486 k ^   N ∙ m 2 C

Passo 3

Agora para calcular a carga basta usar a lei de Gauss:

Φ = q ε 0

q = ε 0 Φ

q = 8,85 x 10 - 12 ∙ - 486 = - 4,3 ∙ 10 - 9 C

Resposta

q = - 4,3 n C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Fluxo e cascas isolantes. Uma partícula carregada está suspensa no centro de duas cascas esféricas concêntricas muito finas, feitas de um material isolante. A F i g .25 - 37 a mostra uma seção reta do
A F i g .25 - 46 a mostra três placas de plástico de grande extensão, paralelas e uniformementecarregadas. AF i g .25 - 46 b mostra a componente x do campo elétrico em função de x . A escala do eixo v
A F i g .25 - 43 mostra pequenas partes de duas linhas de carga paralelas, muito compridas,separadas por uma distância L=8,0c m . A densidade uniforme de carga das linhas é + 6,0μ C / m para a linha 1
A Fig. 25 - 40 mostra uma seção de um tubo longo, de metal, de parede finas, com raio R=3,00 cm e carga por unidade de comprimentoλ=2,00×10 - 8 C / m . Determine o módulo E do campo elétrico a uma dis
Na Fig. 25 - 44 , duas placas finas, condutoras, de grande extensão, são mantidas paralelas a uma pequena distância uma da outra. Nas faces internas, as placas têm densidades superficiais de carga de