Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 21.Problemas desafioadores - Ex. 107
Duas barras delgadas de comprimento estão sobre o eixo , uma delas entre os pontos e e a outra entre os pontos e . Cada barra possui uma carga distribuída uniformemente ao longo de seu comprimento. Calcule o campo elétrico produzido pela segunda barra nos pontos situados ao longo da parte positiva do eixo . Mostre que o módulo da força que uma barra exerce sobre a outra é dado por
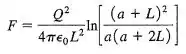
Mostre que, quando , o módulo dessa força se reduz a . (Sugestão: use o desenvolvimento em série , válido para . Faça todos os desenvolvimentos até pelo menos o termo .) Interprete o resultado.
Passo 1
Para calcular o campo elétrico em cada ponto do eixo , podemos considerar um ponto infinitesimal no eixo, assim como um trecho de carga infinitesimal da barra que irá gerar um campo nesse ponto. Então, esboçando essa situação, obtemos:
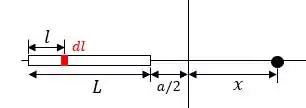
Assim, temos que a distância da carga ao ponto é dada por:
E a carga infinitesimal é:
Essa última equação mostra que a carga diferencial é apenas uma parte infinitesimal de toda a carga distribuída pela barra.
Passo 2
Agora, lembrando que o campo elétrico pode ser dado por:
Transformando em variáveis diferenciais, conseguimos:
Então, integrando essa equação, ou seja, calculando a soma de todos os campos gerados por cargas diferenciais para resultar no campo total, temos:
Ou:
Usando o método da substituição simples com , tal que :
Quando
Quando
Dessa forma:
Passo 3
Da mesma forma, iremos considerar elementos infinitesimais para calcular a força. Assim, sabendo o campo elétrico gerado pela segunda barra, vamos considerar a força que esse mesmo campo exerce sobre uma pequena parcela da carga da primeira barra, que pode ser dada por:
Em seguida, devemos integrar a equação para encontrar a força total exercida pelo segundo campo elétrico em toda a extensão da primeira barra. Portanto:
Fazendo uso da substituição simples com e para o primeiro termo e e para o segundo termo, temos:
Quando e
Quando e
Com isso:
Logo, a força é dada por:
Pelas propriedades de logaritmos, podemos rearranjar a equação como:
Passo 4
Por fim, quando , podemos reorganizar a equação da força de uma forma que possamos representá-la como uma série. Então, reescrevendo a equação da força, temos:
Usando as propriedades de logaritmo, conseguimos dividir o logaritmo original em dois outros:
Ou:
Substituindo por , temos que o valor de é muito pequeno e, com isso, pode ser dado como:
Então, a força é:
Como o valor de é muito maior que , então a variável não terá tanta influência no resultado da força. Portanto: