Enunciado
Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.2 - Ex. 11
Um cilindro maciço e uniforme com massa de e diâmetro de está girando a sobre um eixo delgado e de atrito desprezível, que passa ao longo do eixo de cilindro. Você projeta um freio de atrito simples, que para o cilindro pressionando o freio de encontro à periferia externa com uma força normal. O coeficiente de atrito cinético entre o freio e a periferia é . Qual deve ser a força normal aplicada para colocar o cilindro em repouso após ele ter girado por revoluções?
Passo 1
Fala galera, tudo certo? Pra começar, vamos pensar no problema em si. Temos um cilindro maciço girando em torno do próprio eixo:
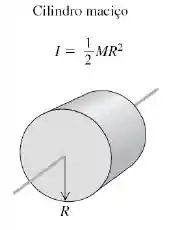
Ai a gente quer parar o cilindro usando um freio. O diagrama de forças desse problema é:
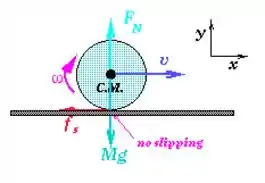
Bem, já que o problema fala de um corpo girando e fala de atrito, isso tudo cheira a momento de inérgia, aceleração angular, torque, etc.
Estamos falando de dinâmica de rotação nééé. Se pegarmos do livro nossa fórmula , vemos que o somatório do torque é dado pelo produto entre o momento de inércia do sistema pela aceleração angular :
E essa fórmula vai nos ajudar a beça! Na figura acima, bora considerar o que parece ser um “chão” na verdade vai ser o nosso freio, beleza?
Passo 2
A força de atrito responsável por freiar o cilindro vai ser, olhando pro diagrama de forças, a única força responsável pelo torque!!
Sendo essa força e o braço de força, como o torque é um produto vetorial, seu módulo será:
Como o ânguulo entre o braço de força e a força de atrito () é de graus...
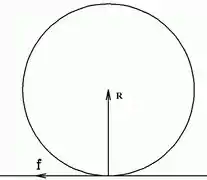
E pela definição de força de atrito:
O torque total será:
E juntando isso á fórmula do livro, temos:
Galera, ta na mão, fórmula da normal, que é o que a questão pede, foi encontrada.
Basta calcular os valores dentro dessa expressão hahaha
Passo 3
A primeira imagem de todas já nos dá um dos nossos pulos do gato: como calcular o momento de inércia! Vale a fórmula:
Do enunciado, temos que:
Calculamos então:
Passo 4
Momento de inércia calculado! A única coisa que não temos ainda é a aceleração angular ()! Pra calcular ela, vamos aplicar a equação:
As considerações agora!! Se o cilindro para de girar, temos que a velocidade angular de rotação final é nula, já que o ato de freiar leva ao repouso:
Passo 5
Inicialmente, o cilindro está girando a , então esse é o nosso . Mas trazendo esse cara pro , podemos fazer a seguinte regra de :
Nossa velocidade angular inicial será:
Passo 6
A gente pode fazer a mesma regra de pra achar . O enunciado diz pra gente que foram revoluções:
Calculando então a aceleração angular, chegamos a:
Passo 7
Agora a gente junta tudo! Nossa normal será:
Onde, do enunciado:
E do passo e :
Assim, a normal valerá: