Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Física de Sears & Zemansky: Mecânica Volume 1 - 12ª Edição - Hugh D. Young e Roger A. Freedman- Ed: 12º - Capítulo 10.4 - Ex. 27

Um carrossel de um parque de diversões possui raio de 2,40   m e momento de inércia igual a 2100   k g ⋅ m 2 em torno de um eixo vertical passando em seu centro e gira com atrito desprezível. a) Uma criança aplica uma força de 18,0   N tangencialmente à periferia do carrossel durante 15,0   s . Se o carrossel está inicialmente em repouso, qual é sua velocidade angular depois deste instante de tempo de 15,0   s ? b) Qual é o trabalho realizado pela criança sobre o carrossel? c) Qual é a potência média fornecida pela criança?

Passo 1

Eaee, belezinha?? Bom... o enunciado nos diz que um carrossel de um parque de diversões possui raio R de 2,40   m e momento de inércia I igual a 2100   k g ⋅ m 2 em torno de um eixo vertical passando em seu centro e gira com atrito desprezível.

Uma criança aplica uma força F de 18,0   N tangencialmente à periferia do carrossel durante 15,0   s .

Queremos calcular a velocidade angular ω depois de 15,0   s após o carrossel partir do repouso.

Em seguida, devemos calcular o trabalho W e a potência média P m e d fornecida pela criança sobre o carrossel.

Para resolvermos essas perguntinhas a gente vai precisar ter em mente que o torque está relacionado com o momento de inércia e a aceleração angular.

E que a força está envolvida nisso!!

Quer saber como??? Bora junto!! 😉

Passo 2

  1. Oi, galerinha! Tudo bom? Vamos começar desenhando o carrossel de cima para entender o que ta acontecendo:

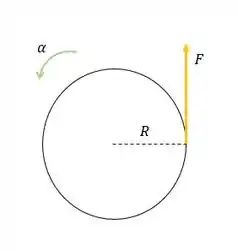
    2. Essa força F amarelinha é justamente onde a criança está empurrando o carrossel.

    Agora vamos aplicar a forma análoga da segunda lei de Newton para a rotação de um corpo rígido:

    ∑ τ = I α

    Para que possamos encontrar a aceleração angular α .

    Assim, temos que:

    F R = I α

    Onde, F é a força aplicada e R , o raio do carrossel.

    Substituindo os valores do enunciado,

    ⇒ α = F R I = 18 N ⋅ 2,40 m 2100 k g ⋅ m 2 = 0,02057 r a d / s 2

    Agora que sabamos a acelaração, vamos achar a velocidade após 15   s ! Lembrando que o carrossel estava em repouso inicialmente

    Passo 3

    Agora, temos os seguintes dados: α = 0,02057 r a d / s 2 t = 15 s ω 0 = 0   ( i n i c i a l m e n t e   e m   r e p o u s o )

    E vamos calcular utilizando a equação:

    ω = ω 0 + α t

    ω = 0 + 0,02057 r a d / s 2 ⋅ 15 s = 0,309 r a d / s

    Pronto! Vamos para letra b.

    Passo 4

  2. Utilizando a equação do trabalho realizado por um torque constante:

    3. W = τ θ 2 - θ 1 = τ Δ θ

    Então, primeiro, vamos calcular Δ θ :

    Δ θ = ω 0 t + 1 2 α t 2 = 0 + 1 2 ( 0,02057 r a d / s 2 ) ⋅ ( 15 s ) = 2314 r a d

    E agora, calcular τ :

    τ = F R = 18 N ⋅ 2,40 m = 43,2 N ⋅ m

    Então,

    W = τ ∆ θ = 43,2 N ⋅ m ⋅ 2314 r a d = 100   J

    Passo 5

  3. Para calcular a potencia media, vamos usar a equação:

P m é d i a = ∆ W ∆ t = 100 J 15 s = 6,67 w a t t s

Resposta

  1. ω = 0,309 r a d / s
  2. W = 100   J
  3. P m é d i a = 6,67 w a t t s
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Oito alunos de física, cujos pesos estão indicados em newtons na Figura, se equilibram em uma gangorra. Qual é o número do estudante que produz o maior torque em relação a um eixo de rotação que passa
Oito alunos de física, cujos pesos estão indicados em newtons na Figura, se equilibram em uma gangorra. Qual é o número do estudante que produz o maior torque em relação a um eixo de rotação que passa
O corpo da figura abaixo, pode girar em torno de um eixo que passa por O e é perpendicular ao papel e está submetido a três forças: FA=10 N no ponto A, a 8,0 m de O; FB=16 N em B, a 4,0 m de O; e FC=1
Um esmeril de 50,0 kg é um disco sólido de diâmetro igual a 0,520 m. Você comprime um machado sobre a periferia com uma força normal de 160 N (Figura 10.43). O coeficiente de atrito cinético entre a l
O comprimento do braço do pedal de uma bicicleta é 0,152 m e uma força de 111 N é aplicada ao pedal pelo ciclista. Qual é o módulo do torque em relação ao eixo do braço do pedal quando o braço faz um