Enunciado

Física - Moysés - Vol. 3- Ed: 1º - Capítulo 8.Problemas - Ex. 6

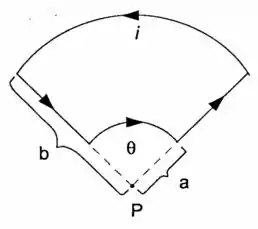
O circuito da figura, formado por sois latos retilíneos e dois arcos de círculo, subtendendo um setor circular de ângulo , é percorrido por uma corrente de intensidade . Calcule o campo magnético no ponto (centro do setor circular).

Passo 1

Se liga! Podemos perceber que as correntes causadas pela parte reta estão indo na direção do ponto. Sendo assim, usando o argumento que

podemos dizer que o campo produzido pelas partes retas na figura é zero.

Passo 2

Agora vamos analisar as partes correspondentes ao setor circular. Veja a figura!

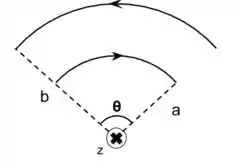
Repare que, pela regra da mão direita, o campo produzido pelo setor circular maior está saindo na direção e o do menor está entrando. Consideraremos que o eixo é positivo entrando.

Sabemos que

Como temos um setor circular adotaremos que

Então, para o setor de raio , teremos

Passo 3

Para o campo do setor de raio menos, vamos colocar o campo com o sinal de menos.

Passo 4

Agora só precisamos somar

Pronto!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A espira retangular da figura, de lados a e b , é percorrida por uma corrente i . Calcule a força F → exercida sobre ela por um fio retilíneo longo, que transporta uma corrente i ' , situado à uma dis

Nas figs. (a) e (c), as porções retilíneas dos fios são supostas muito longas e a porção semicircular tem raio R . A corrente tem intensidade i . Calcule o campo B → , em módulo, direção e sentido, no

Duas bobinas circulares coaxiais idênticas, de espessura desprezível, com N espiras de raio a em cada bobina, transportam correntes de mesma intensidade i e mesmo sentido, e estão colocados uma acima

Uma espira em forma de retângulo, de lados 2 a e 2 b , transportam uma corrente de intensidade i .Calcule a magnitude do campo magnético no centro do retângulo.Tome o limite do resultado para a ≫ b e