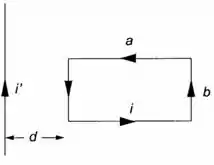
A espira retangular da figura, de lados e , é percorrida por uma corrente . Calcule a força exercida sobre ela por um fio retilíneo longo, que transporta uma corrente , situado à uma distância da espira (dê módulo, direção e sentido).
Passo 1
Se liga! A primeira coisa que precisamos lembrar para solucionar esta questão é que
Agora, precisamos lembrar que o campo magnético produzido por um fio é dado por
Para facilitar o que falaremos mais a frente, vamos montar um desenho nomeando os segmentos da espira.
Os segmentos 1 e 3 não sofrem força, pois são perpendiculares ao fio. Já os segmentos 2 e 4 sentem. Outra coisa, temos que lembrar que a atração ocorre quando temos correntes no mesmo sentido, já a repulsão quando temos sentido contrário.
Passo 2
Então, agora só precisamos calcular a força nos segmentos 2 e 4. Vamos começar pelo 2.
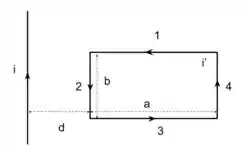
Considerando que para o segmento 2 e comprimento varia de
Passo 3
Repare que para o segmento 4, o que muda é que a corrente estará no mesmo sentido do fio e . Sendo assim, temos
Passo 4
Agora só precisamos somar. Consideraremos o sentido da força de mais intensidade como positivo e o outro negativo,
Pronto!